
【题目】在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数. 小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答.

问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?

(提示:过点P作PE∥AD),请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
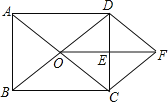
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,求组成的两位数是4的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).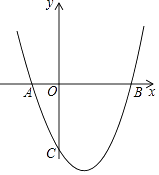
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,
求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,直接写出使△QBC为直角三角形的点Q的
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵.若购进1棵A种树苗与2棵B种树苗共需200元;购进2棵A种树苗与1棵B种树苗共需220元.
(1)求购进A种树苗和B种树苗每棵各多少元?
(2)若小区购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(3)若购进B种树苗的数量少于A种树苗的数量,请设计一种费用最省的方案,并求出该方案所需费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
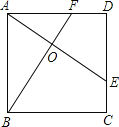
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
下面是一个有关平行四边形和等边三角形的小实验,请根据实验解答问题:
已知在□ABCD中,∠ABC=120°,点D又是等边三角形DEF的一个顶点,DE与AB相交于点M,DF与BC相交于点N(不包括线段的端点).
(1)初步尝试:
如图①,若AB=BC,求证:BD=BM+BN;
(2)探究发现:
如图②,若BC=2AB,过点D作DH⊥BC于点H,求证:∠BDC=90°.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com