
【题目】将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,求组成的两位数是4的倍数的概率.
【答案】
(1)解:∵随机地抽取一张,所有可能的情况是:1,2,3三种,且它们出现的可能性相等.而结果出现奇数的有1,3两种,
∴P(奇数)= ![]()
(2)解:根据题意画树状图如下:

则组成的两位数有:12、13、21、23、31、32,其中是4的倍数的有12、32,
从而所求概率P= ![]() =
= ![]()
【解析】(1)先求出这组数中奇数的个数,再利用概率公式解答即可;(2)根据题意列举出能组成的数的个数及组成的两位数是4的倍数的个数,再利用概率公式解答.
【考点精析】本题主要考查了列表法与树状图法的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,面积为48 cm2的正方形的四个角是面积为3 cm2的小正方形,请动手操作,将四个角剪掉,制作一个无盖的长方体盒子,求这个长方体盒子的底面边长.

【答案】![]()
【解析】试题分析:根据算术平方根的定义求出大正方形和小正方形的边长,再根据底边边长的表示列式计算即可得解.
试题解析:解:正方形的边长=![]() =
=![]() cm,剪掉小正方形的边长=
cm,剪掉小正方形的边长=![]() cm,所以,长方体盒子的底面边长=
cm,所以,长方体盒子的底面边长=![]() =
=![]() (cm).
(cm).
答:这个长方体盒子的底面边长是![]() cm.
cm.
点睛:本题考查了二次根式的应用,主要利用了算术平方根的定义,以及二次根式的运算.
【题型】解答题
【结束】
26
【题目】已知![]() 求(1)x2-xy+y2;(2)x3y+xy3的值.
求(1)x2-xy+y2;(2)x3y+xy3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
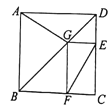
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=60°,点P为BC边上一点,设BP=x,AP2=y(如图1),已知y是x的二次函数的一部分,其图象如图2所示,点Q(2,12)是图象上的最低点.
(1)边AB= , BC边上的高AH=;
(2)当△ABP为直角三角形时,BP的长是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某停车场收费标准分为中型汽车和小型汽车两种,某两天这个停车场的收费情况如下表:
中型汽车数量 | 小型汽车数量 | 收取费用 | |
第一天 | 15辆 | 35辆 | 360元 |
第二天 | 18辆 | 20辆 | 300元 |
(1)中型汽车和小型汽车的停车费每辆多少元?
(2)某天停车场共停车70辆,若收取的停车费用高于500元,则中型汽车至少有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点(﹣2,﹣2)和点(2,4).
(1)求这个函数的解析式;
(2)判断点P(1,1)是否在此函数图象上,并说明理由.
(3)求这个函数的图象与坐标轴围成的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=![]() ∠BMN
∠BMN
同理∠GNM=![]() ∠DNM.
∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
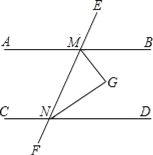
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com