练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，∠B=60°，点P为BC边上一点，设BP=x，AP2=y（如图1），已知y是x的二次函数的一部分，其图象如图2所示，点Q（2，12）是图象上的最低点．

    （1）边AB= ， BC边上的高AH=；
    （2）当△ABP为直角三角形时，BP的长是多少．

    【答案】
    （1）4；2
    （2）

    解：当∠APB=90°时，在△ABP中，∠B=60°，

    ∴∠BAP=30°，∴BP= AB=2；

    当∠BAP=90°时，在△ABP中，∠B=60°，

    ∴∠APB=30°，

    ∴BP=2AB=8．

    综上可知当△ABP为直角三角形时，BP的长是2或8


    【解析】解：（1）当AP⊥BC时可知AP2最小，
    ∵函数图象中过Q点时函数值最小，
    ∴AH= =2 ，即BC边上的高为2 ；
    在Rt△ABH中，∠B=60°，
    ∴ =sin60°，即 = ，解得AB=4，
    所以答案是：4；2 ；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系．

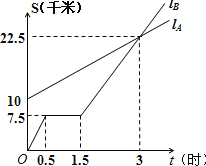
    （1）B出发时与A相距 千米．

    （2）走了一段路后，自行车发生故障，进行修理，所用的时间是 小时．

    （3）B出发后 小时与A相遇．

    （4）求出A行走的路程S与时间t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点 A(2，0)，B(0，4),点 C 在第一象限.

    （1）如图 1，连接 AB、BC、AC，∠OBC=90°，∠BAC=2∠ABO,求点 C 的坐标；

    （2）动点 P 从点 B 出发，以每秒 2 个单位的速度沿 x 轴负方向运动，连接 AP，设 P 点的 运动时间为 t 秒，△AOP 的面积为 S，用含 t 的式子表示 S，并直接写出 t 的取值范围；

    （3）如图 2，在（1）条件下，点 P 在线段 OB 上，连接 AP、PC,AB 与 PC 相交于点 Q,当S=3, ∠BAC=∠BPC 时，求△ACQ 的面积.

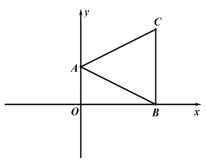
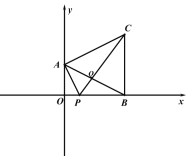
    图 1 图 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：（1）如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数. 小颖同学的解题思路是：如图2，过点P作PE∥AB，请你接着完成解答.

    问题迁移：

    （2）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．试判断∠CPD、∠α、∠β之间有何数量关系？

    （提示：过点P作PE∥AD），请说明理由；

    （3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你猜想∠CPD、∠α、∠β之间的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作正方形ADEF，连接CF．

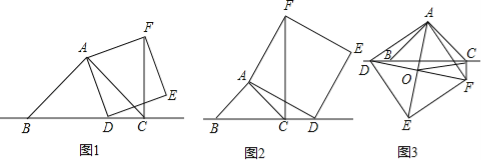
    （1）如图1，当点D在线段BC上时，求证：①BD⊥CF．②CF=BC﹣CD．

    （2）如图2，当点D在线段BC的延长线上时，其它条件不变，请直接写出CF、BC、CD三条线段之间的关系；

    （3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系．②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

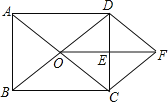
    【题目】已知：如图，在矩形ABCD中，对角线AC、BD相交于点O，E是CD中点，连结OE．过点C作CF∥BD交线段OE的延长线于点F，连结DF．求证：

    （1）△ODE≌△FCE；

    （2）四边形ODFC是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上．
    （1）随机地抽取一张，求P（奇数）；
    （2）随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，求组成的两位数是4的倍数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为响应市政府“创建国家森林城市”的号召，某小区计划购进A、B两种树苗共17棵．若购进1棵A种树苗与2棵B种树苗共需200元；购进2棵A种树苗与1棵B种树苗共需220元．

    （1）求购进A种树苗和B种树苗每棵各多少元？

    （2）若小区购进A、B两种树苗刚好用去1220元，问购进A、B两种树苗各多少棵？

    （3）若购进B种树苗的数量少于A种树苗的数量，请设计一种费用最省的方案，并求出该方案所需费用？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD和四边形ACED都是平行四边形，点R在DE上，且DR：RE=5：4，BR分别与AC，CD相交于点P，Q，则BP：PQ：QR= ．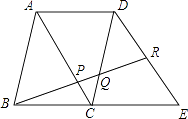

    查看答案和解析>>

    同步练习册答案