【题目】如图，四边形ABCD和四边形ACED都是平行四边形，点R在DE上，且DR：RE=5：4，BR分别与AC，CD相交于点P，Q，则BP：PQ：QR= ．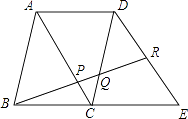 
【答案】7：2：5
【解析】解：∵四边形ABCD和四边形ACED都是平行四边形，
∴BC=AD=CE，AC∥DE，
∴PB=PR， 
，
又∵PC∥DR，
∴△PCQ∽△RDQ，
∴ 
，
∵DR：RE=5：4，
∴RE= 
DR，
∴ = 
，
∴QR= 
PQ，
又∵BP=PR=PQ+QR= 
PQ，
∴BP：PQ：QR=7：2：5，
所以答案是：7：2：5．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)，还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键．
科目：初中数学 来源： 题型：
【题目】在△ABC中，∠B=60°，点P为BC边上一点，设BP=x，AP2=y（如图1），已知y是x的二次函数的一部分，其图象如图2所示，点Q（2，12）是图象上的最低点．
（1）边AB= ， BC边上的高AH=；
（2）当△ABP为直角三角形时，BP的长是多少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数的图象经过点（﹣2，﹣2）和点（2，4）．
（1）求这个函数的解析式；
（2）判断点P（1，1）是否在此函数图象上，并说明理由．
（3）求这个函数的图象与坐标轴围成的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（-8，0）及动点P（x，y），且2x-y＝-6.设三角形OPA的面积为S.
（1）当x＝-2时，点P坐标是____________；
（2）若点P在第二象限，且x为整数时，求y的值；
（3）是否存在第一象限的点P，使得S＝12.若存在，求点P的坐标；若不存在，
说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，甲、乙两艘轮船同时从港口O出发，甲轮船以20海里/时的速度向南偏东45°方向航行，乙轮船向南偏西45°方向航行．已知它们离开港口O两小时后，两艘轮船相距50海里，求乙轮船平均每小时航行多少海里？
查看答案和解析>>
科目：初中数学 来源： 题型：
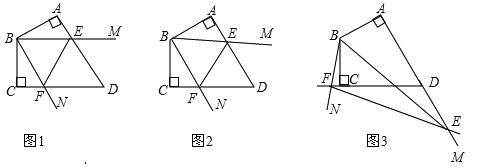
【题目】已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．
当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；
当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
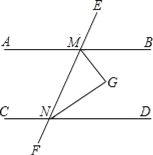
【题目】如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
（1）完成下面的证明：
∵MG平分∠BMN
∴∠GMN=
∠BMN
同理∠GNM=
∠DNM．
∵AB∥CD ，
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
（2）把上面的题设和结论，用文字语言概括为一个命题： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
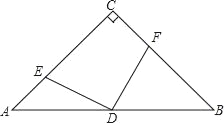
【题目】已知：如图，在△ABC中，∠ACB=90°，AC=BC，D是AB的中点，点E在AC上，点F在BC上，且AE=CF．
（1）求证：DE=DF，DE⊥DF；
（2）若AC=2，求四边形DECF面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示．例如f(x)＝x2＋3x－5，把x＝某数时多项式的值用f(某数)来表示．例如x＝－1时多项式x2＋3x－5的值记为f(－1)＝(－1)2＋3×(－1)－5＝－7.
(1)已知g(x)＝－2x2－3x＋1，分别求出g(－1)和g(－2)；
(2)已知h(x)＝ax3＋2x2－ax－6，当h(
)＝a，求a的值；
(3)已知f(x)＝
－
－2(a，b为常数)，当k无论为何值，总有f(1)＝0，求a，b的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com