
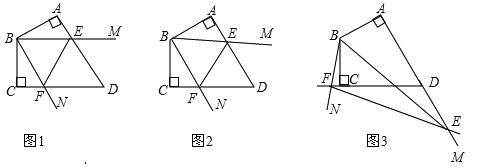
【题目】已知四边形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;
当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
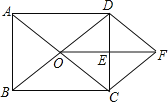
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
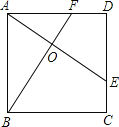
【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示为一张长为m,宽为n(m<n)的小长方形纸片,现将8张该纸片按如图2所示的方式无缝隙不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分面积差为S,当BC长度变化时,按照同样的方式放置,S却始终保持不变,则此时![]() =______.
=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R在DE上,且DR:RE=5:4,BR分别与AC,CD相交于点P,Q,则BP:PQ:QR= . 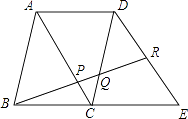
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2(y6)2-(y4)3; (2)(ab2c)2÷(ab3c2);
(3)(-x-y)(x-y)+(x+y)2 (4)利用公式计算803×797;
(5)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
下面是一个有关平行四边形和等边三角形的小实验,请根据实验解答问题:
已知在□ABCD中,∠ABC=120°,点D又是等边三角形DEF的一个顶点,DE与AB相交于点M,DF与BC相交于点N(不包括线段的端点).
(1)初步尝试:
如图①,若AB=BC,求证:BD=BM+BN;
(2)探究发现:
如图②,若BC=2AB,过点D作DH⊥BC于点H,求证:∠BDC=90°.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com