
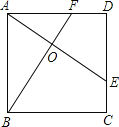
【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
A.1个 B.2个 C.3个 D.4个
【答案】A
【解析】
试题分析:根据四边形ABCD是正方形及CE=DF,可证出△ADE≌△BAF,则得到:①AE=BF,以及△ADE和△BAF的面积相等,得到;④S△AOB=S四边形DEOF;可以证出∠ABO+∠BAO=90°,则②AE⊥BF一定成立.错误的结论是:③AO=OE.
解:∵四边形ABCD是正方形,
∴CD=AD
∵CE=DF
∴DE=AF
∴△ADE≌△BAF
∴AE=BF(故①正确),S△ADE=S△BAF,∠DEA=∠AFB,∠EAD=∠FBA
∵S△AOB=S△BAF﹣S△AOF,
S四边形DEOF=S△ADE﹣S△AOF,
∴S△AOB=S四边形DEOF(故④正确),
∵∠ABF+∠AFB=∠DAE+∠DEA=90°
∴∠AFB+∠EAF=90°
∴AE⊥BF一定成立(故②正确).
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
∴,假设不成立,AO≠OE(故③错误);
故错误的只有一个.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡度是tanα=![]() ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).

查看答案和解析>>
科目:初中数学 来源: 题型:
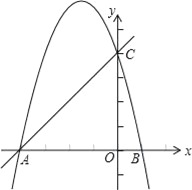
【题目】如图,抛物线y=ax2﹣bx﹣4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
(1)求抛物线的解析式,并用配方法把其化为y=a(x﹣h)2+k的形式,写出顶点坐标;
(2)已知点D(m,1﹣m)在第二象限的抛物线上,求出m的值,并直接写出点D关于直线AC的对称点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面上,正方形ABCD的四个顶点到直线l的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l可以有( )
A. 4条 B. 8条 C. 12条 D. 16条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:(2+a)(2-a)+a(a-2b)+3a5b÷(-a2b)4,其中ab=-![]() .
.
(2)因式分解:a(n-1)2-2a(n-1)+a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,
①如果梯子的顶端下滑了1m,那么梯子的底端也向后滑动1m吗?请通过计算解答.
②梯子的顶端从A处沿墙AO下滑的距离与点B向外移动的距离有可能相等吗?若有可能,请求出这个距离,没有可能请说明理由.
③若将上题中的梯子换成15米长的直木棒,将木棒紧靠墙竖直放置然后开始下滑直至直木棒的顶端A滑至墙角O处,试求出木棒的中点Q滑动的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com