
【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
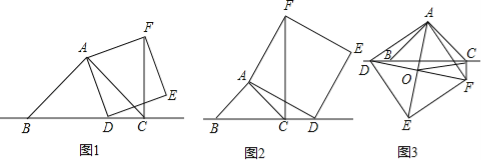
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
【答案】(1)证明见解析;(2)CF=BC+CD;(3)①CF=CD-BC;②△AOC是等腰三角形.理由见解析.
【解析】试题分析:(1)、①、根据等腰直角的性质得出∠ABC=∠ACB=45°,从而得出四边形ADEF是正方形,根据∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°得出∠BAD=∠CAF,从而得出△BAD和△CAF全等,则∠ACF=∠ABD=45°,从而得出垂直;②、根据 全等得出BD=CF,从而得出结论;(2)、根据(1)的证法的采购员BD=CF,得出CF=BC+CD;(3)、①、根据(1)的证法得出BD=CF,从而得出CF=CD-BC;②、∠BAC=90°,AB=AC得出∠ABD=135°,根据四边形ADEF是正方形得出∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,从而得出△BAD和△CAF全等,则∠ACF=135°,从而得出∠FCD=∠ACF-∠ACB=90°,得出△FCD为直角三角形,根据正方形的性质得出OC=OA,从而说明△FCD为等腰直角三角形.
试题解析:(1)、①、∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°, ∴∠BAD=∠CAF,
在△BAD和△CAF中, AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°, ∴∠ACF+∠ACB=90°, ∴BD⊥CF;
②、由①△BAD≌△CAF可得BD=CF, ∵BD=BC-CD, ∴CF=BC-CD;
(2)、与(1)同理可得BD=CF, 所以,CF=BC+CD;
(3)、①、与(1)同理可得,BD=CF, 所以,CF=CD-BC;
②∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, 则∠ABD=180°-45°=135°,
∵四边形ADEF是正方形, ∴AD=AF,∠DAF=90° ∵∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,
∴∠BAD=∠CAF, 在△BAD和△CAF中,AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°, ∴∠FCD=∠ACF-∠ACB=90°,则△FCD为直角三角形,
∵正方形ADEF中,O为DF中点, ∴OC=![]() DF ∵在正方形ADEF中,OA=
DF ∵在正方形ADEF中,OA=![]() AEAE=DF, ∴OC=OA,
AEAE=DF, ∴OC=OA,
∴△AOC是等腰三角形


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图.

依据图中信息,得出下列结论:
(1)接受这次调查的家长人数为200人
(2)在扇形统计图中,“不赞同”的家长部分所对应的扇形圆心角大小为162°
(3)表示“无所谓”的家长人数为40人
其中正确的结论个数为( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
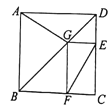
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两同学用两枚质地均匀的骰子作游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局. 根据上述规则,解答下列问题;
(1)随机掷两枚骰子一次,用列表法求点数和为8的概率;
(2)甲先随机掷两枚骰子一次,点数和是7,求乙随机掷两枚骰子一次获胜的概率. (骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=60°,点P为BC边上一点,设BP=x,AP2=y(如图1),已知y是x的二次函数的一部分,其图象如图2所示,点Q(2,12)是图象上的最低点.
(1)边AB= , BC边上的高AH=;
(2)当△ABP为直角三角形时,BP的长是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某停车场收费标准分为中型汽车和小型汽车两种,某两天这个停车场的收费情况如下表:
中型汽车数量 | 小型汽车数量 | 收取费用 | |
第一天 | 15辆 | 35辆 | 360元 |
第二天 | 18辆 | 20辆 | 300元 |
(1)中型汽车和小型汽车的停车费每辆多少元?
(2)某天停车场共停车70辆,若收取的停车费用高于500元,则中型汽车至少有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com