
【题目】在平面直角坐标系中,点 A(2,0),B(0,4),点 C 在第一象限.
(1)如图 1,连接 AB、BC、AC,∠OBC=90°,∠BAC=2∠ABO,求点 C 的坐标;
(2)动点 P 从点 B 出发,以每秒 2 个单位的速度沿 x 轴负方向运动,连接 AP,设 P 点的 运动时间为 t 秒,△AOP 的面积为 S,用含 t 的式子表示 S,并直接写出 t 的取值范围;
(3)如图 2,在(1)条件下,点 P 在线段 OB 上,连接 AP、PC,AB 与 PC 相交于点 Q,当S=3, ∠BAC=∠BPC 时,求△ACQ 的面积.
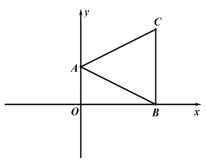
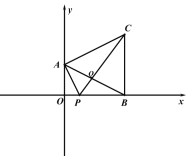
图 1 图 2
【答案】(1)C(4,4);(2)![]() ;(3)
;(3) ![]() .
.
【解析】分析: (1) 作AD⊥BC于D,可得D(4,2),BD=2,根据△ABD≌△ACD,得BC=4,从而
可知C点坐标.
(2)分两种情况根据三角形的面积公式即可求出,一种是当![]() 时,此时点P在OB上;另一种是点P在x轴负半轴上运动时,此时
时,此时点P在OB上;另一种是点P在x轴负半轴上运动时,此时![]() .
.
(3) 作AE⊥PC于E,作BF⊥PC于F,作CG⊥AB于G,可得BP=3,OP=1,由(1)中△ABD≌△ACD得AB=AC,易证△ACE≌△ABO, △AOP≌△AEP,从而得PC=5由面积法,可求BF=2.4,从而AE:BF=5:6由面积法得![]() ,因此
,因此![]() .
.
详解:
(1) 过点A作AD⊥BC于D,
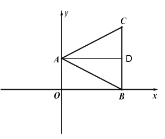
∵点 A(2,0),B(0,4), ∠OBC=90°,
∴D(4,2),
∴BD=2,
∵∠BAC=2∠ABO,
∴∠BAD=∠CAD,
又∵AD=AD, ∠ADB=∠ADC,
∴△ABD≌△ACD,
∴BC=4,
∴C(4,4)
(2)当点P在OB上时,![]() ,
,
由题意得OA=2,OP=4-2t,
∴S=2×(4-2t) ×![]() =4-2t;
=4-2t;
当点P在x轴负半轴上时,![]() ,
,
由题意得OA=2,OP=2t- 4,
∴S=2×(2t- 4) ×![]() =2t- 4;
=2t- 4;
综上,![]()
(3) 作AE⊥PC于E,作BF⊥PC于F,作CG⊥AB于G
∵S=3,
∴可得BP=3,OP=1
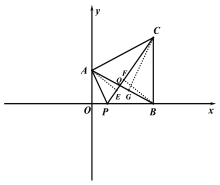
由(1)△ABD≌△ACD
∴AB=AC
∵∠BAC=∠BPC
∴∠ACP=∠ABP
易证△ACE≌△ABO,
△AOP≌△AEP,
∴CE=BO=4,OP=EP=1,
AO=AE=2
∴PC=5(1分)
由面积法,可求BF=2.4
∴AE:BF=5:6
由面积法, ![]()
∴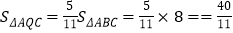


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某企业生产部统计了15名工人某月加工的零件数:
![]()
(1)写出这15人该月加工的零件数的平均数、中位数和众数;
(2)若生产部领导把每位工人的月加工零件数定为260件,你认为是否合理,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为48 cm2的正方形的四个角是面积为3 cm2的小正方形,请动手操作,将四个角剪掉,制作一个无盖的长方体盒子,求这个长方体盒子的底面边长.

【答案】![]()
【解析】试题分析:根据算术平方根的定义求出大正方形和小正方形的边长,再根据底边边长的表示列式计算即可得解.
试题解析:解:正方形的边长=![]() =
=![]() cm,剪掉小正方形的边长=
cm,剪掉小正方形的边长=![]() cm,所以,长方体盒子的底面边长=
cm,所以,长方体盒子的底面边长=![]() =
=![]() (cm).
(cm).
答:这个长方体盒子的底面边长是![]() cm.
cm.
点睛:本题考查了二次根式的应用,主要利用了算术平方根的定义,以及二次根式的运算.
【题型】解答题
【结束】
26
【题目】已知![]() 求(1)x2-xy+y2;(2)x3y+xy3的值.
求(1)x2-xy+y2;(2)x3y+xy3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在直角坐标系中,
在直角坐标系中,
![]() 请写出
请写出![]() 各点的坐标.
各点的坐标.
![]() 若把
若把![]() 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到![]() ,写出
,写出![]() 、
、![]() 、
、![]() 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形.
![]() 求出三角形ABC的面积.
求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( ) 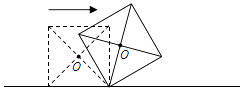
A.4a
B.2 ![]() πa
πa
C.![]() πa
πa
D.![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
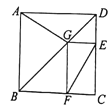
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=60°,点P为BC边上一点,设BP=x,AP2=y(如图1),已知y是x的二次函数的一部分,其图象如图2所示,点Q(2,12)是图象上的最低点.
(1)边AB= , BC边上的高AH=;
(2)当△ABP为直角三角形时,BP的长是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点(﹣2,﹣2)和点(2,4).
(1)求这个函数的解析式;
(2)判断点P(1,1)是否在此函数图象上,并说明理由.
(3)求这个函数的图象与坐标轴围成的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com