
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).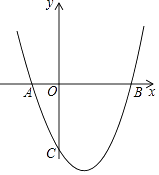
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,
求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,直接写出使△QBC为直角三角形的点Q的
坐标.
【答案】
(1)
解:∵A(﹣1,0),C(0,﹣3)在y=x2+bx+c上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴二次函数的解析式为y=x2﹣2x﹣3
(2)
解:在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=3或x=﹣1,
∴B(3,0),且C(0,﹣3),
∴经过B、C两点的直线为y=x﹣3,
设点P的坐标为(x,x2﹣2x﹣3),如图,过点P作PD⊥x轴,垂足为D,与直线BC交于点E,则E(x,x﹣3),

∵S四边形ABPC=S△ABC+S△BCP= ![]() ×4×3+
×4×3+ ![]() (3x﹣x2)×3=﹣
(3x﹣x2)×3=﹣ ![]() x2+
x2+ ![]() x+6=
x+6= ![]() ,
,
∴当 ![]() 时,四边形ABPC的面积最大,此时P点坐标为(
时,四边形ABPC的面积最大,此时P点坐标为( ![]() ,﹣
,﹣ ![]() ),
),
∴四边形ABPC的最大面积为 ![]()
(3)
解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为x=1,
∴可设Q点坐标为(1,t),
∵B(3,0),C(0,﹣3),
∴BQ2=(1﹣3)2+t2=t2+4,CQ2=12+(t+3)2=t2+6t+10,BC2=18,
∵△QBC为直角三角形,
∴有∠BQC=90°、∠CBQ=90°和∠BCQ=90°三种情况,
① 当∠BQC=90°时,则有BQ2+CQ2=BC2,即t2+4+t2+6t+10=18,解得t= ![]() 或t=
或t= ![]() ,此时Q点坐标为(1,
,此时Q点坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
②当∠CBQ=90°时,则有BC2+BQ2=CQ2,即t2+4+18=t2+6t+10,解得t=2,此时Q点坐标为(1,2);
③当∠BCQ=90°时,则有BC2+CQ2=BQ2,即18+t2+6t+10=t2+4,解得t=﹣4,此时Q点坐标为(1,﹣4);
综上可知Q点的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,2)或(1,﹣4).
)或(1,2)或(1,﹣4).
【解析】(1)把A、C两点坐标代入可求得b、c的值,可求得二次函数的解析式;(2)由抛物线解析式可求得B点坐标,由B、C坐标可求得直线BC解析式,可设出P点坐标,用P点坐标表示出四边形ABPC的面积,根据二次函数的性质可求得其面积的最大值及P点坐标;(3)由抛物线解析式可求得其对称轴,则可设出Q点的坐标,则可表示出QB2、QC2和BC2 , 分∠BQC=90°、∠CBQ=90°和∠BCQ=90°三种情况,分别根据勾股定理得到关于Q点坐标的方程,可求得Q点的坐标.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC=4cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为 . 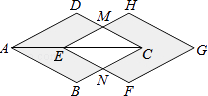
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着裕安中学的规模逐渐扩大,学生人数越来越多,学校打算购买校车20辆,现有A和B两种型号校车,如果购买A型号校车6辆,B型号14辆,需要资金580万元;如果购买A型号校车12辆,B型号校车8辆,需要资金760万元.已知每种型号校车的座位数如表所示:
A型号 | B型号 | |
座位数(个/辆) | 60 | 30 |
经预算,学校准备购买设备的资金不高于500万元.(每种型号至少购买1辆)
(1)每辆A型校车和B型校车各多少万元?
(2)请问学校有几种购买方案?且哪种方案的座位数最多,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | 50 | 0.25 |
四 | 80.5~90.5 | m | 0.40 |
五 | 90.5~100.5 | n |
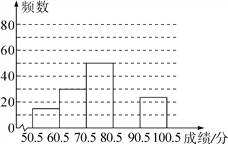
(1)本次抽样调查的样本是__________,样本容量为__________,表中m=__________,n=__________;
(2)补全频数分布直方图;
(3)若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班组织去方特参加秋季社会实践活动,其中第一小组有x人,第二小组的人数比第一小组人数的![]() 少30人,如果从第二小组调出10人到第一小组,那么:
少30人,如果从第二小组调出10人到第一小组,那么:
(1)两个小组共有多少人?
(2)调动后,第一小组的人数比第二小组多多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com