
【题目】随着裕安中学的规模逐渐扩大,学生人数越来越多,学校打算购买校车20辆,现有A和B两种型号校车,如果购买A型号校车6辆,B型号14辆,需要资金580万元;如果购买A型号校车12辆,B型号校车8辆,需要资金760万元.已知每种型号校车的座位数如表所示:
A型号 | B型号 | |
座位数(个/辆) | 60 | 30 |
经预算,学校准备购买设备的资金不高于500万元.(每种型号至少购买1辆)
(1)每辆A型校车和B型校车各多少万元?
(2)请问学校有几种购买方案?且哪种方案的座位数最多,是多少?
【答案】(1)每辆A型校车50万元,每辆B型校车20万元;(2)共有3种购买方案;购买A型3辆,B型17辆时座位数最多,是690个.
【解析】(1)根据购买A型号校车6辆,B型号14辆,需要资金580万元;购买A型号校车12辆,B型号校车8辆,需要资金760万元.得出等量关系,列出二元一次方程组即可;(2) 根据学校打算购买校车20辆,而可用于购买设备的资金不高于500万元,可得出不等式关系,求出即可.
(1)设每辆A型校车![]() 万元,每辆B型校车
万元,每辆B型校车![]() 万元,则
万元,则
![]() ,解得
,解得![]()
答:每辆A型校车50万元,每辆B型校车20万元
(2)设学校购买A型校车a辆,则购买B型校车(20-a)辆
![]()
解得![]() .又∵每种型号至少购买1辆
.又∵每种型号至少购买1辆
∴a可取1,2,3,有三种购买方案.
方案一:购买A型1辆,B型19辆,座位数:1×60+19×30=630(个)
方案二:购买A型2辆,B型18辆,座位数:2×60+18×30=660(个)
方案三:购买A型3辆,B型17辆,座位数:3×60+17×30=690(个)
答:共有3种购买方案;购买A型3辆,B型17辆时座位数最多,是690个.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
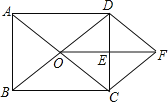
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点. 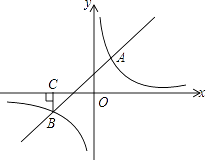
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标. 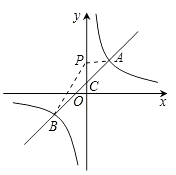
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).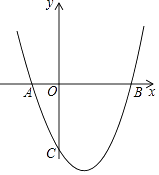
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,
求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,直接写出使△QBC为直角三角形的点Q的
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E. 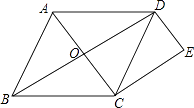
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2(y6)2-(y4)3; (2)(ab2c)2÷(ab3c2);
(3)(-x-y)(x-y)+(x+y)2 (4)利用公式计算803×797;
(5)计算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com