
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF﹣GF,DF=CD﹣FC,
∴EG=DF,
故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中,
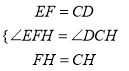 ,
,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°,
故②正确;
③由②知:△EHF≌△DHC,
故③正确;
④∵![]() ,
,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,
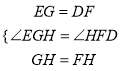 ,
,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示:
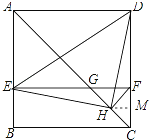
设HM=x,则CF=2x,
∴DF=2FC=4x,
∴DM=5x,DH=![]() x,CD=6x,
x,CD=6x,
则S△CFH=![]() ×HM×CF=
×HM×CF= ![]() x2x=x2 , S△EDH=
x2x=x2 , S△EDH= ![]() ×DH2=
×DH2= ![]() ×
×![]() =13x2,
=13x2,
∴则S△EDH=13S△CFH ,故④正确;
其中结论正确的有:①②③④,4个,
故选D.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
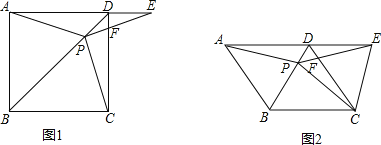
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC=4cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为 . 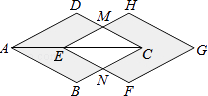
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.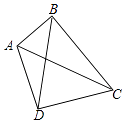
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: ![]() .
.
(3)①若AB=BC=4,AD+DC=6,求 ![]() 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( ) 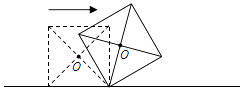
A.4a
B.2 ![]() πa
πa
C.![]() πa
πa
D.![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着裕安中学的规模逐渐扩大,学生人数越来越多,学校打算购买校车20辆,现有A和B两种型号校车,如果购买A型号校车6辆,B型号14辆,需要资金580万元;如果购买A型号校车12辆,B型号校车8辆,需要资金760万元.已知每种型号校车的座位数如表所示:
A型号 | B型号 | |
座位数(个/辆) | 60 | 30 |
经预算,学校准备购买设备的资金不高于500万元.(每种型号至少购买1辆)
(1)每辆A型校车和B型校车各多少万元?
(2)请问学校有几种购买方案?且哪种方案的座位数最多,是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com