
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
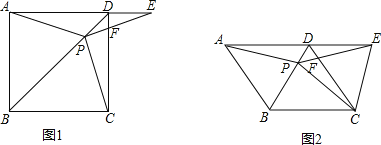
【答案】(1)证明见试题解析;(2)90°;(3)AP=CE.
【解析】试题分析:(1)、根据正方形得出AB=BC,∠ABP=∠CBP=45°,结合PB=PB得出△ABP ≌△CBP,从而得出结论;(2)、根据全等得出∠BAP=∠BCP,∠DAP=∠DCP,根据PA=PE得出∠DAP=∠E,即∠DCP=∠E,然后根据180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E得出答案;(3)、首先证明△ABP和△CBP全等,然后得出PA=PC,∠BAP=∠BCP,然后得出∠DCP=∠E,从而得出∠CPF=∠EDF=60°,然后得出△EPC是等边三角形,从而得出AP=CE.
试题解析:(1)、在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,又∵ PB=PB ∴△ABP ≌△CBP(SAS), ∴PA=PC,∵PA=PE,∴PC=PE;
(2)、由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,
∵PA=PE, ∴∠DAP=∠E, ∴∠DCP=∠E, ∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E, 即∠CPF=∠EDF=90°;
(3)、AP=CE
理由是:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中, 又∵ PB=PB ∴△ABP≌△CBP(SAS), ∴PA=PC,∠BAP=∠BCP,
∵PA=PE,∴PC=PE,∴∠DAP=∠DCP, ∵PA=PC ∴∠DAP=∠E, ∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等), ∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°, ∴△EPC是等边三角形,∴PC=CE,∴AP=CE


科目:初中数学 来源: 题型:
【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
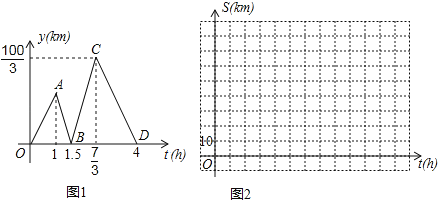
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过![]() h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列选项中,具有相反意义的量是( )
A.收入20元与支出30元
B.上升了6米和后退了7米
C.卖出10斤米和盈利10元
D.向东行30米和向北行30米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,50,55,这组数据的众数和中位数分别是( ).
A. 50元,30元B. 50元,40元
C. 50元,50元D. 55元,50元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为申办2013年冬奥会,须改变某城市的交通状况,在街道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.问:距离B点8米元的保护物是否存在危险?
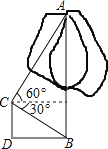
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com