
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.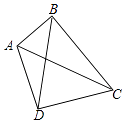
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: ![]() .
.
(3)①若AB=BC=4,AD+DC=6,求 ![]() 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值.
【答案】
(1)
解:结论:AB2+BC2=AD2+DC2.
理由:∵∠ABC=∠ADC=90°,
∴AB2+BC2=AC2,BC2+DC2=AC2,
∴AB2+BC2=AD2+DC2
(2)
解:如图1中,过点B作AD的垂线BE交DA的延长线于点E,
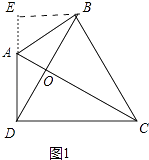
∵∠ABC=∠ADC=90°,
∴∠ADC+∠ABC=180°,
∴四边形ABCD四点共圆,
∴∠BDE=∠ACB,∠EAB=∠BCD,
∵∠BED=∠ABC=90°,
∴△BED∽△ABC,
∴ ![]() =
= ![]() =sin∠EAB=sin∠BCD
=sin∠EAB=sin∠BCD
(3)
解:①如图2中,过点B作BF⊥BD交DC的延长线于F.
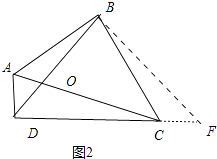
∵∠ABC=∠DBF=90°,∠BAD+∠BCD+∠ABC+∠ADC=360°,∠ABC+∠ADC=180°,
∴∠BAD=180°﹣∠BCD=∠BCF,
∵∠BCF=∠BAD,BC=BA,
∴△DAB≌△CBF,
∴BD=BF,AD=CF,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴BD= ![]() DF,
DF,
∵AD+CD=6,
∴CF+CD=DF=6,
∴BD=3 ![]() ,AC=
,AC= ![]() =4
=4 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
②当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为NM延长BA交MN于点N,则四边形DCNM是矩形,△ABM∽△BCN,
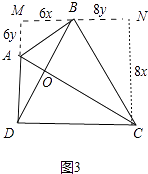
∴ ![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,
,设AM=6y,BN=8y,BM=6x,CN=8x,
在Rt△BDM中,BD= ![]() =10x,
=10x,
∵BD=DC,
∴10x=6x+8y,
∴x=2y,
在Rt△DABM中,AB= ![]() =6
=6 ![]() y,
y,
∴sin∠BCD=sin∠MAB= ![]() =
= ![]() =
= ![]()
【解析】(1)结论:AB2+BC2=AD2+DC2 , 根据勾股定理即可证明.(2)如图1中,过点B作AD的垂线BE交DA的延长线于点E,只要证明△BED∽△ABC,即可解决问题.(3)①如图2中,过点B作BF⊥BD交DC的延长线于F.只要证明△DAB≌△CBF,推出DF=AD+CD=6,求出BD、AC即可.
②当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为NM延长BA交MN于点N,则四边形DCNM是矩形,△ABM∽△BCN,所以 ![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,通过BD=DC,列出方程求出x、y的关系,求出AB,即可解决问题.
,设AM=6y,BN=8y,BM=6x,CN=8x,通过BD=DC,列出方程求出x、y的关系,求出AB,即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)

解:垂直.理由如下:
∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°( 垂直的意义 ).
∴DE∥BC( ① )
∴∠1=∠DCB( ② )
∵∠1与∠2互补(已知).
∴∠DCB与∠2互补
∴ ③ (同旁内角互补,两直线平行)
∴∠BFH=∠CDB( ④ )
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFH= ⑤ ( ⑥ ).
∴HF⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
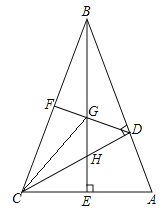
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,连接CG,∠ABE=∠CBE.
(1)求证:BH=AC;
(2)若BG=5,GE=4,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过对角线BD中点的直线交AD、BC边于F、E. 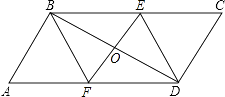
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,写出EF与BD的关系.
(3)若∠A=60°,AB=4,BC=6,四边形BEDF是矩形,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李到某城市行政中心大楼办事,假定乘电梯向上一楼记为+1,向下一楼记为–1.
小李从1楼出发,电梯上下楼层依次记录如下(单位:层): +5,–3,+10,–8,+12,–6,–10.
(1)请你通过计算说明小李最后是否回到出发点1楼;
(2)该中心大楼每层高2.8m,电梯每上或下1m需要耗电0.1度.根据小李现在所处的位置,请你算一算,当他办事时电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E. 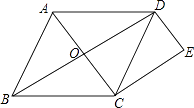
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com