
【题目】小李到某城市行政中心大楼办事,假定乘电梯向上一楼记为+1,向下一楼记为–1.
小李从1楼出发,电梯上下楼层依次记录如下(单位:层): +5,–3,+10,–8,+12,–6,–10.
(1)请你通过计算说明小李最后是否回到出发点1楼;
(2)该中心大楼每层高2.8m,电梯每上或下1m需要耗电0.1度.根据小李现在所处的位置,请你算一算,当他办事时电梯需要耗电多少度?
科目:初中数学 来源: 题型:
【题目】现有5个质地、大小完全相同的小球上分别标有数字-1,-2,1,2,3.先将标有数字-2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现分别从两个盒子里各随即取出一个小球.
(1)请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果;
(2)求取出的两个小球上的数字之和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,AC 是对角线,AB=CD,∠DAC+∠BCA=180°,∠BAC+∠ACD=90°,四边形 ABCD 的面积是 18,则 CD 的长是__________.
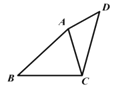
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.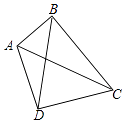
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: ![]() .
.
(3)①若AB=BC=4,AD+DC=6,求 ![]() 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CE⊥AB于点E,DF⊥AB于点F,CE平分∠ACB,DF平分∠BDE,
求证:AC∥ED.
证明:∵CE⊥AB于E,DF⊥AB于F(已知)
∴DF∥ (垂直于同一条直线的两直线平行)
∴∠BDF=∠ ( )
∠FDE=∠ (两直线平行,内错角相等)
∵CE平分∠ACB,DF平分∠BDE(已知)
∴∠ACE=∠ECB,∠EDF=∠BDF(角平分线的定义)
∴∠ACE=∠ (等量代换)
∴AC∥ED( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2+(2m+1)x+2(m为实数). 
(1)请探究该函数图象与x轴的公共点个数的情况(要求说明理由);
(2)在图中给出的平面直角坐标系中分别画出m=﹣1和m=1的函数图象,并根据图象直接写出它们的交点坐标;
(3)探究:对任意实数m,函数的图象是否一定过(2)中的点,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.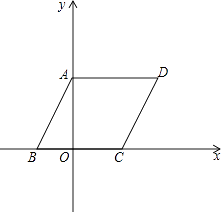
(1)求OA、OB的长.
(2)若点E为x轴正半轴上的点,且S△AOE= ![]() ,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com