
【题目】如图,在△ABC中,CE⊥AB于点E,DF⊥AB于点F,CE平分∠ACB,DF平分∠BDE,
求证:AC∥ED.
证明:∵CE⊥AB于E,DF⊥AB于F(已知)
∴DF∥ (垂直于同一条直线的两直线平行)
∴∠BDF=∠ ( )
∠FDE=∠ (两直线平行,内错角相等)
∵CE平分∠ACB,DF平分∠BDE(已知)
∴∠ACE=∠ECB,∠EDF=∠BDF(角平分线的定义)
∴∠ACE=∠ (等量代换)
∴AC∥ED( ).

【答案】CE;BCE;两直线平行,同位角相等;DEC;DEC;内错角相等,两直线平行.
【解析】根据垂直证明DF∥CE,利用平行线的性质和角平分线的定义得出∠ACE=∠DEC,进而利用平行线判定解答即可.
详证明:∵CE⊥AB于E,DF⊥AB于F(已知)
∴DF∥CE(垂直于同一条直线的两直线平行)
∴∠BDF=∠BCE(两直线平行,同位角相等)
∠FDE=∠DEC(两直线平行,内错角相等)
∵CE平分∠ACB,DF平分∠BDE(已知)
∴∠ACE=∠ECB,∠EDF=∠BDF(角平分线的定义)
∴∠ACE=∠DEC(等量代换)
∴AC∥ED(内错角相等,两直线平行).
故答案为:CE;BCE;两直线平行,同位角相等;DEC;DEC;内错角相等,两直线平行.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,购进 4 件甲种商品比购进 5 件乙种商品少用 10 元,购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
(1)求甲、乙两种商品每件进价分别是多少元?
(2)若该商店购进甲、乙两种商品共 140 件,都标价 10 元出售,售出一部分降价促销, 以标价的八折售完所有剩余商品,以 10 元售出的商品件数比购进甲种商品件数少 20 件,该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元,求至少购进甲种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李到某城市行政中心大楼办事,假定乘电梯向上一楼记为+1,向下一楼记为–1.
小李从1楼出发,电梯上下楼层依次记录如下(单位:层): +5,–3,+10,–8,+12,–6,–10.
(1)请你通过计算说明小李最后是否回到出发点1楼;
(2)该中心大楼每层高2.8m,电梯每上或下1m需要耗电0.1度.根据小李现在所处的位置,请你算一算,当他办事时电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
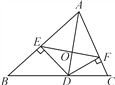
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上运动(不与点
上运动(不与点![]() 、
、![]() 重合),点
重合),点![]() 在射线
在射线![]() 上运动,且
上运动,且![]() ,设
,设![]() .
.
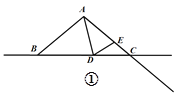
(1)如图①,当点![]() 在边
在边![]() 上时,且
上时,且![]() ,则
,则![]() _______,
_______,![]() _______;
_______;
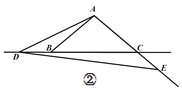
(2)如图②,当点![]() 运动到点
运动到点![]() 的左侧时,其他条件不变,请猜想
的左侧时,其他条件不变,请猜想![]()
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
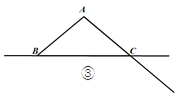
(3)当点![]() 运动到点C的右侧时,其他条件不变,
运动到点C的右侧时,其他条件不变,![]() 和
和![]() 还满足(2)
还满足(2)
中的数量关系吗?请画出图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a=![]() ,
,![]() ,c是-27的立方根.
,c是-27的立方根.
(1)b =_______,c =_______;
(2)化简a,并求a+b-c的平方根;
(3)若关于![]() 的不等式组
的不等式组![]() 无解,求
无解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com