
����Ŀ������ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
��1����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ����֤���١�ADC�ա�CEB����DE=AD+BE��
��2����ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ����֤��DE=AD��BE��
��3����ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ������DE��AD��BE���������ĵ�����ϵ����д�����������ϵ��������֤����

���𰸡���1��֤������������2��֤������������3��DE=BE��AD��
����������1������֪AC=BC����ADC=��CEB=90�㣬���û����ϵ��֤��DAC=��ECB����֤��ACD�ա�CBE����AD=CE��CD=BE����AD+BE=CE+CD=DE����2����ʱ�����С�ACD�ա�CBE��AD=CE��CD=BE�������߶εĺͲ��ϵ��DE=AD-BE��
֤������1���ߡ�ADC=��ACB=��BEC=90�㣬
���CAD+��ACD=90�㣬��BCE+��CBE=90�㣬��ACD+��BCE=90�㣮
���CAD=��BCE��
��AC=BC��
���ADC�ա�CEB��
��CE=AD��CD=BE��
��DE=CE+CD=AD+BE��
��2��DE=AD��BE
֤�����ߡ�ADC=��CEB=��ACB=90�㣬
���ACD=��CBE��
�֡�AC=BC��
���ACD�ա�CBE��
��CE=AD��CD=BE��
��DE=CE��CD=AD��BE��
��3��DE=BE��AD����AD=BE��DE��BE=AD+DE�ȣ���
��֤�á�ACD�ա�CBE��
��AD=CE��DC=BE��
��DE=CD- CE =BE��AD��
���㾦�����⿼��������ת��Ѱ��֤��������ȫ�ȵ��������ؼ�������ȫ�������ζ�Ӧ�߶���ȣ����й��߶ν���ת����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ε�һ�߳�Ϊ3����һ�߳�Ϊ6���������ܳ�Ϊ ( )
A. 9 B. 12 C. 15 D. 12��15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BE��CF�ֱ���AC��AB�����ϵĸߣ���BE�Ͻ�ȡBD=AC����CF���ӳ����Ͻ�ȡCG=AB������AD��AG��
��1����֤��AD=AG��
��2��AD��AG��λ�ù�ϵ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
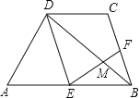
����Ŀ�� ��ͼ������ABCD�У�AB//CD����AB=2CD��E��F�ֱ���AB��BC���е㣮
EF��BD�ཻ�ڵ�M��
��1����֤����EDM�ס�FBM��
��2����DB=9����BM��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ���ڡ�����Σ�շ����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ�˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������ˣ�
��1������ѡȡ�����ķ����������һ���� ����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����γ������˷��֣����ܵ��˵ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��
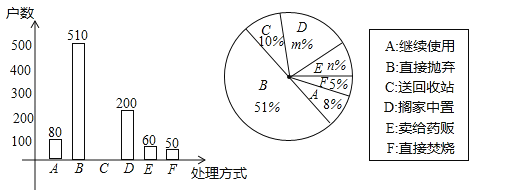
��m= ��n= ��
����ȫ����ͳ��ͼ��
�����ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��
����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε�һ�ߵ���3��һ�ߵ���6����ô�����ܳ�����_______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и�ʽ�У��루a��b��2һ����ȵ��ǣ� ��
A.a2+2ab+b2
B.a2��b2
C.a2+b2
D.a2��2ab+b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������a��b��c�������϶�Ӧ���λ����ͼ��ʾ��������и��⣺
��1���ж����и�ʽ�ķ��ţ�������������������
a��b�� ��0��b��c�� ��0��c��a�� ��0��b+c�� ��0
��2������|a��b|+|b��c|��|c��a|+|b+c|��
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com