
【题目】一次函数y=kx+b图象经过点(0,3)和(4,7).
①试求k与b;
②画出这个一次函数图象;
③这个一次函数与x轴交点坐标是_____;
④当x_____时,y<0;
⑤当x_____时,y>0;
⑥当0<y<7时,x的取值范围是_____.
【答案】①k=1,b=3;②图象见解析;③(-3,0);④<-3;⑤>-3;⑥-3.
【解析】试题分析:①将(0,3)和(4,7)分别代入代入y=kx+b,联立解方程可得k和b的值;
②根据函数经过(0,3)和(4,7)两点可确定函数图象;
③根据(1)所求的解析式令y=0即可求出与x轴交点的坐标;
④观察图象即可得;
⑤观察图象即可得;
⑥将y=0、y=7分别代入(1)中的解析式即可得.
试题解析:①把点(0,3)和(4,7)代入y=kx+b得![]() ,解得
,解得![]() ;
;
②函数的图象如图:
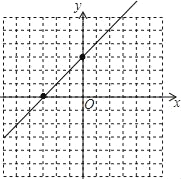
③由①可知:y=x+3,令y=0,则有x+3=0,解得:x=-3,所以图象与x轴的交点坐标为(﹣3,0),
故答案为:(-3,0);
④观察图象可知当x<﹣3时,y<0,
故答案为<-3;
⑤观察图象可知当x>﹣3时,y>0,
故答案为>-3;
⑥y=0时,0=x+3,解得:x=-3,
y=7时,7=x+3,解得:x=4,
所以当0<y<7时,x的取值范围是﹣3<x<4,
故答案为:﹣3<x<4.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() ,
, ![]() 为“相伴数对”,记为
为“相伴数对”,记为![]() .
.
(1)若![]() 是“相伴数对”,求
是“相伴数对”,求![]() 的值;
的值;
(2)写出一个“相伴数对” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴数对”,求代数式
是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个正方形边长分别为a、b.
(1)求阴影部分的面积.
(2)如果a+b=17,ab=60,求阴影部分的面积.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/17/1904284875390976/1906414662729728/STEM/433f25b861984b60a78ae031a98667fa.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
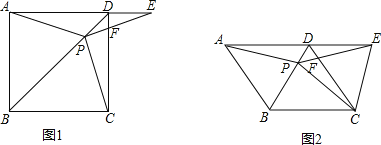
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC=4cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为 . 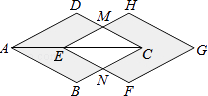
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com