
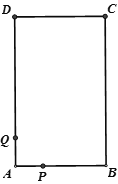
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?

【答案】(1)2;(2)4秒或8秒;(3)t=2.5秒,4.5秒,7.5秒或9.5秒.
【解析】
(1)当t=3秒时,点P运动到线段BC上,即可得到BP的长度;
(2)由△ABP的面积为长方形的面积三分之一,则分为点P在BC上和点P在AD上两大类进行讨论,即可得到答案;
(3)根据题意,要使得一个三角形与△DCQ全等,则点P的位置可以有四个,即点P分别运动到P1,P2,P3 ,P4时,有△DCP1,△ABP2,△ABP3,△DCP4与△DCQ全等,根据P点运动的位置,即可计算出时间.
解:(1)当t=3秒时,
点P走过的路程为:![]() ,
,
∵AB=4,
∴点P运动到线段BC上,
∴BP=6-4=2;
(2)∵矩形ABCD的面积=![]() ,
,
∴△ABP的面积=![]() ,
,
∵AB=4,
∴△ABP的高为:![]() ,
,
如图:
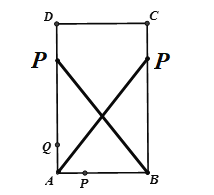
当点P在BC上时,有BP=4,
∴时间为:![]() s;
s;
当点P在AD上时,有AP=4,
∴时间为:![]() s;
s;
∴当时间t=4s或t=8s时,△ABP的面积为长方形的面积三分之一;
(3)根据题意,如图,连接CQ,有AB=CD=4,∠A=∠B=∠C=∠D=90°,DQ=5,
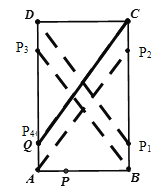
∴要使得一个三角形与△DCQ全等,则另一直角边必须等于DQ.
①当点P运动到P1时,CP1=DQ=5,此时△DCQ≌△CDP1,
∴点P的路程为:AB+BP1=4+1=5,
∴时间![]() ;
;
②当点P运动到P2时,BP2= DQ=5,此时△CDQ≌△ABP2,
∴点P的路程为:AB+BP2=4+5=9,
∴时间![]() ;
;
③当点P运动到P3时,AP3= DQ=5,此时△CDQ≌△ABP3,
∴点P的路程为:AB+BC+CD+DP3=4+6+4+1=15,
∴时间![]() ;
;
④当点P运动到P4时,即P与Q重合时,DP4=DQ=5,△CDQ≌△CDP4,
∴点P的路程为:AB+BC+CD+DP4=4+6+4+5=19,
∴时间![]() ;
;
综合上述,时间t的值可以是:t=2.5秒,4.5秒,7.5秒或9.5秒.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】以下是一位同学所做的有理数运算解题过程的一部分:
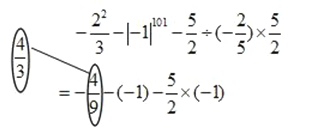
(1)请你在上面的解题过程中仿照给出的方式,圈画出他的错误之处,并将正确结果写在相应的圈内;
(2)请就此题反映出的该同学有理数运算掌握的情况进行具体评价,并对相应的有效避错方法给出你的建议。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)当m取何值时,此方程有两个不相等的实数根;
(2)当抛物线y=mx2+(3m+1)x+3与x轴两个交点的横坐标均为整数,且m为正整数时,求此抛物线的解析式;
(3)在(2)的条件下,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象直接写出实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
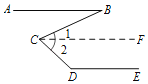
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°.
证明:过点C作CF∥AB.
∵CF∥AB(已作),
∴∠1= .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE
∴∠D+∠2=180°
∴∠D+∠BCD﹣∠B=180° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将任意三个互不相等的数a,b,c按照从小到大的顺序排列后,把处于中间位置的数叫做这三个数的中位数.用符号mid{a,b,c}表示.例如mid{﹣1,2,1}=1.
(1)mid{![]() ,5,3}= .
,5,3}= .
(2)当x<﹣2时,求mid{1+x,1﹣x,﹣1}.
(3)若x≠0,且mid{5,5﹣2x,2x+1}=2x+1,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数![]() 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为![]() ,
,![]() ,
,![]() 的三角形是“和谐三角形”
的三角形是“和谐三角形”
概念理解:
如图,![]() ,在射线
,在射线![]() 上找一点
上找一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为端点作射线
为端点作射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与
不与![]() 重合)
重合)
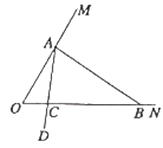
(1)![]() 的度数为 ,
的度数为 ,![]() (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”
(2)若![]() ,求证:
,求证:![]() 是“和谐三角形”.
是“和谐三角形”.
应用拓展:
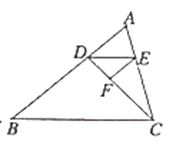
如图,点![]() 在
在![]() 的边
的边![]() 上,连接
上,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于48棵,且用于购买这两种树的资金不能超过7500元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)由大小相同的小立方块搭成的几何体如图1,请在图2的方格中画出该几何体的俯视图和左视图.
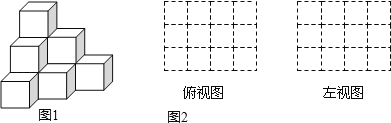
(2)用小立方体搭一个几何体,使得它的俯视图和左视图与你在方格中所画的一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com