
【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数![]() 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为![]() ,
,![]() ,
,![]() 的三角形是“和谐三角形”
的三角形是“和谐三角形”
概念理解:
如图,![]() ,在射线
,在射线![]() 上找一点
上找一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为端点作射线
为端点作射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与
不与![]() 重合)
重合)
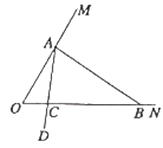
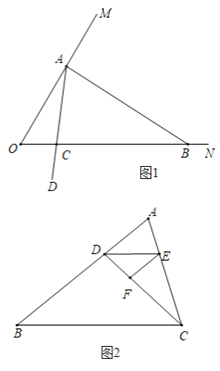
(1)![]() 的度数为 ,
的度数为 ,![]() (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”
(2)若![]() ,求证:
,求证:![]() 是“和谐三角形”.
是“和谐三角形”.
应用拓展:
如图,点![]() 在
在![]() 的边
的边![]() 上,连接
上,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() 的度数.
的度数.
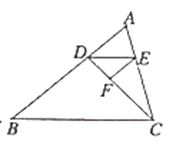
【答案】(1)![]() °,是;(2)见解析;(3)
°,是;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“和谐三角形”的概念判断;
(2)根据三角形外角的性质求出![]() 的度数,然后根据“和谐三角形”的概念证明即可;
的度数,然后根据“和谐三角形”的概念证明即可;
应用拓展:首先易证∠EFC=∠ADC,根据平行线的性质得到∠DEF=∠ADE,推出DE∥BC,得到∠CDE=∠BCD,根据角平分线的定义得到∠ADE=∠CDE,求得∠B=∠BCD,然后根据“和谐三角形”的定义求解即可.
解: (1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为“和谐三角形”,
为“和谐三角形”,
故答案为:![]() °;是;
°;是;
(2)证明:∵![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是“和谐三角形”;
是“和谐三角形”;
应用拓展:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是“和谐三角形”,
是“和谐三角形”,
∴![]() ,或
,或![]() ,
,
∵![]() ,
,
∴![]() 或
或![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与⊙O相切;
(2)如果PD=![]() ,求AP的长.
,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陶军于上周购买某农产品10000斤,每斤![]() 元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤
元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤![]() 元)
元)
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天的价格涨跌情况(元) |
|
|
|
|
|
当天的交易量(斤) | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品价格为每斤多少元?
(2)本周内该农产品的最高价格为每斤多少元?最低价格为每斤多少元?
(3)陶军在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
科目:初中数学 来源: 题型:
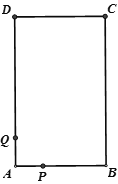
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
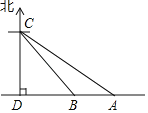
【题目】据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.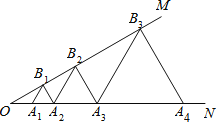
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( )
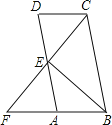
A. FA:FB=1:2 B. AE:BC=1:2
C. BE:CF=1:2 D. S△ABE:S△FBC=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利.但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”.随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别 | 观点 | 频数(人数) |
| 损坏零件 | 50 |
| 破译密码 | 20 |
| 乱停乱放 |
|
| 私锁共享单车,归为己用 |
|
| 其他 | 30 |
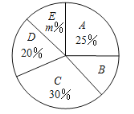
请根据以上信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;
(2)求扇形图中![]() 组所在扇形的圆心角度数;
组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有![]() 组观点的市民人数.
组观点的市民人数.
(4)针对以上现象,作为初中生的你有什么合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com