Question

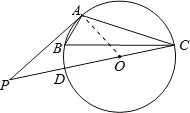
【题目】如图，已知A、B、C分别是⊙O上的点，∠B=60°，P是直径CD的延长线上的一点，且AP=AC．

（1）求证：AP与⊙O相切；

（2）如果PD=，求AP的长．

Answer 1

【答案】（1）证明参见解析；（2）3．

【解析】

试题分析：（1）利用圆周角定理以及等腰三角形的性质,得出∠P=∠ACP=∠OCA=∠OAC=30°，∠PAC=120°，进而得出∠PAO=90°，即可得出答案；（2）首先根据直角三角形中30°角所对的直角边等于斜边的一半求得半径，从而求得OA、OP，进而利用勾股定理得出AP的长．

试题解析：（1）如图：连接AO，

∵∠B=60°，∴∠AOC=120°，∵AO=CO，AP=AC，∴∠P=∠ACP，∠OCA=∠OAC=30°，∴∠P=∠ACP=∠OCA=∠OAC=30°，∴∠PAC=120°，∴∠PAO=90°，∴AP是⊙O的切线；（2）设⊙O的半径为R，则OA=OD=R，PD=，∴OP=+R，∵∠PAO=90°，∠P=30°，∴OP=2OA，即+R=2R，解得R=，∴OA=，OP=2，根据勾股定理得：PA=,AP===3．故AP长为3.