
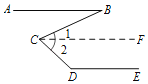
【题目】完成下面的证明.
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°.
证明:过点C作CF∥AB.
∵CF∥AB(已作),
∴∠1= .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE
∴∠D+∠2=180°
∴∠D+∠BCD﹣∠B=180° .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
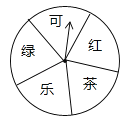
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陶军于上周购买某农产品10000斤,每斤![]() 元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤
元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤![]() 元)
元)
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天的价格涨跌情况(元) |
|
|
|
|
|
当天的交易量(斤) | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品价格为每斤多少元?
(2)本周内该农产品的最高价格为每斤多少元?最低价格为每斤多少元?
(3)陶军在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
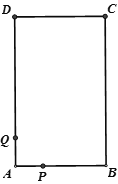
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.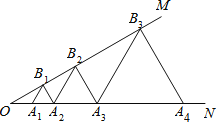
查看答案和解析>>
科目:初中数学 来源: 题型:
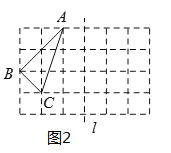
【题目】(1)如图②,利用网格线画![]() ,使它与
,使它与![]() 关于直线
关于直线![]() 对称.若每个小正方形边长为1,则
对称.若每个小正方形边长为1,则![]() 的面积为__.
的面积为__.
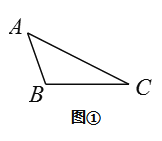
(2)如图①,用直尺和圆规在△ABC的一边![]() 上确定一点
上确定一点![]() ,使PC=PB.若△ABP的周长为16,BC=8,则△ABC的周长为__.
,使PC=PB.若△ABP的周长为16,BC=8,则△ABC的周长为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com