
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)当m取何值时,此方程有两个不相等的实数根;
(2)当抛物线y=mx2+(3m+1)x+3与x轴两个交点的横坐标均为整数,且m为正整数时,求此抛物线的解析式;
(3)在(2)的条件下,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象直接写出实数a的取值范围.
【答案】(1)当m≠![]() 且m≠0时,方程有两个不相等的实数根;(2)y=x2+4x+3;(3) 当y1>y2时,a>1,或a<-5.
且m≠0时,方程有两个不相等的实数根;(2)y=x2+4x+3;(3) 当y1>y2时,a>1,或a<-5.
【解析】
(1)根据一元二次方程的定义和一元二次方程根的判别式进行分析解答即可;
(2)用公式法求得关于x的一元二次方程mx2+(3m+1)x+3=0的两根,再结合已知条件求得m的值即可得到抛物线的解析式;
(3)根据(2)中所得抛物线的解析式,画出函数的图象,根据图象结合已知条件即可求得对应的a的取值范围.
(1)由题意可知,Δ=b2-4ac=(3m+1)2-4m×3=(3m-1)2>0,
解得:m≠![]() ,
,
∵mx2+(3m+1)x+3=0是一元二次方程,
∴m≠0,
∴当m≠![]() 且m≠0时,关于x的一元二次方程mx2+(3m+1)x+3=0有两个不相等的实数根;
且m≠0时,关于x的一元二次方程mx2+(3m+1)x+3=0有两个不相等的实数根;
(2)由一元二次方程的求根公式可解得mx2+(3m+1)x+3=0的两实数根为:x1=-3,x2=![]() .
.
∵抛物线与x轴两个交点的横坐标均为整数,且m为正整数,
∴m=1,
∴抛物线的解析式为y=x2+4x+3;
(3)画出函数y=x2+4x+3的图象如下图所示;
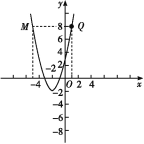
当x=1时,y=1+4+3=8,由此可得图中点Q的坐标为(1,8),
过点Q作y轴的垂线,交抛物线于点M,
根据抛物线的对称性,可得点M(-5,8),
由图象可知,当y1>y2时,a>1,或a<-5.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与⊙O相切;
(2)如果PD=![]() ,求AP的长.
,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
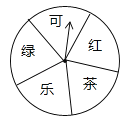
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(![]() ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
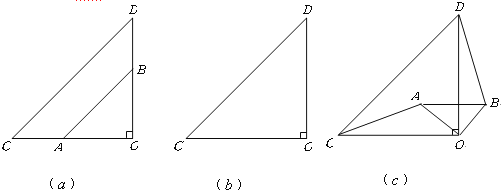
(1)将图(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角,在图(
角,在图(![]() )中作出旋转后的
)中作出旋转后的![]() (保留作图痕迹,不写作法,不证明).
(保留作图痕迹,不写作法,不证明).
(2)在图(![]() )中,你发现线段
)中,你发现线段![]() ,
,![]() 的数量关系是 ,直线
的数量关系是 ,直线![]() ,
,![]() 相交成 度角.
相交成 度角.
(3)将图(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转一个锐角,得到图(
顺时针旋转一个锐角,得到图(![]() ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若![]() 绕点
绕点![]() 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陶军于上周购买某农产品10000斤,每斤![]() 元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤
元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤![]() 元)
元)
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天的价格涨跌情况(元) |
|
|
|
|
|
当天的交易量(斤) | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品价格为每斤多少元?
(2)本周内该农产品的最高价格为每斤多少元?最低价格为每斤多少元?
(3)陶军在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
科目:初中数学 来源: 题型:
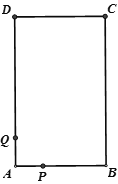
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利.但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”.随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别 | 观点 | 频数(人数) |
| 损坏零件 | 50 |
| 破译密码 | 20 |
| 乱停乱放 |
|
| 私锁共享单车,归为己用 |
|
| 其他 | 30 |
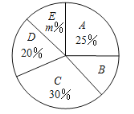
请根据以上信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;
(2)求扇形图中![]() 组所在扇形的圆心角度数;
组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有![]() 组观点的市民人数.
组观点的市民人数.
(4)针对以上现象,作为初中生的你有什么合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com