
【题目】如图所示,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是________.(只写出符合要求的一个即可)

【答案】点D在∠BAC的平分线上(或AE=AF)
【解析】
首先根据题意画出图形,然后由DE∥AC、DF∥AB,判定四边形DEAF为平行四边形,再由菱形的判定定理求解即可求得答案.
添加点D在∠BAC的平分线上(或AE=AF).
如图,连接AD.
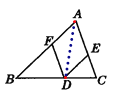
∵DF∥AC、DE∥AB,
∴四边形AFDE为平行四边形.
①当添加点D在∠BAC的平分线上时.
∵AD平分∠BAC,DE∥AB,
∴∠BAD=∠CAD,∠BAD=∠ADE,
∴∠CAD=∠ADE,
∴AE=DE,
∵四边形AFDE为平行四边形,
∴四边形AFDE为菱形;
②当添加AE=AF时.
∵四边形AFDE为平行四边形,AE=AF,
∴四边形AFDE为菱形.
故答案为:点D在∠BAC的平分线上(或AE=AF).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中给定以下五个点A(-2,0),B(1,0),C(4,0),D![]() ,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
,E(0,-6),从这五个点中选取三点,使经过三点的抛物线满足以y轴的平行线为对称轴.我们约定经过A,B,E三点的抛物线表示为抛物线ABE.
(1)符合条件的抛物线共有多少条?不求解析式,请用约定的方法一一表示出来.
(2)在五个形状、颜色、质量完全相同的乒乓球上标上A,B,C,D,E代表以上五个点,玩摸球游戏,每次摸三个球.请问:摸一次,三球代表的点恰好能确定一条符合条件的抛物线的概率是多少?
(3)小强、小亮用上面的五球玩游戏,若符合要求的抛物线开口向上,小强可以得1分;若抛物线开口向下,小亮得5分,你认为这个游戏谁获胜的可能性大一些?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y(米)与小明打完电话后的步行时间t(分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有 .(把正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程.
已知:线段 a, b.

求作:等腰△ABC,使线段 a 为腰,线段 b 为底边 BC 上的高. 作法:如图,

①画直线 l,作直线 m⊥l,垂足为 P;
②以点 P 为圆心,线段 b 的长为半径画弧,交直线 m 于点 A;
③以点 A 为圆心,线段 a 的长为半径画弧,交直线 l 于 B,C 两点;
④分别连接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ = ,
∴△ABC 为等腰三角形( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,点A,B的坐标分别为(-2,0),(1,0).同时将点A ,B先向左平移1个单位长度,再向上平移2个单位长度,得到点A,B的对应点依次为C,D,连接CD,AC, BD .
(1)写出点C , D 的坐标;
(2)在 y 轴上是否存在点E,连接EA ,EB,使S△EAB=S四边形ABDC?若存在,求出点E的坐标;若不存在,说明理由;
(3)点 P 是线段 AC 上的一个动点,连接 BP , DP ,当点 P 在线段 AC 上移动时(不与 A , C 重合),直接写出CDP 、ABP 与BPD 之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于F.

(1)如图1,连CF,求证:∠ABE=∠ACF;
(2)如图2,当∠ABC=60°时,求证:AF+EF=FB;
(3)如图3,当∠ABC=45°时,若BD平分∠ABC,求证:BD=2EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
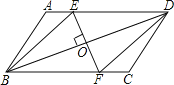
【题目】已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.

(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com