
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F,若∠C=30°,DF=2,求BD的长.

【答案】6.
【解析】
根据已知利用AAS判定△ABD≌△ACE,则AD=AE,∠B=∠C,因为AB=AC,可得BE=CD,再利用AAS判定△BEF≌△CDF,则BF=CF,BD=DF+CF,根据含30°的直角三角形的性质可得CF=2DF,即可求解.
解:∵AB=AC,BD⊥AC于D,CE⊥AB于E,
∴∠ADB=∠AEC=90°,∠BAD=∠CAE,
∴△ABD≌△ACE.
∴AD=AE,∠B=∠C,
∵AB = AC,
∴AC-AD=AB-AE.
∴BE=CD
又∵∠B=∠C,∠EFB=∠DFC,
∴△BEF≌△CDF,
∴BF=CF,则BD=DF+CF,
∵BD⊥AC于D,∠C=30°,DF=2,
∴CF=2DF=4,
∴BD=DF+CF=2+4=6.


科目:初中数学 来源: 题型:
【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么可以用数学语言表达:
,那么可以用数学语言表达:![]() .
.
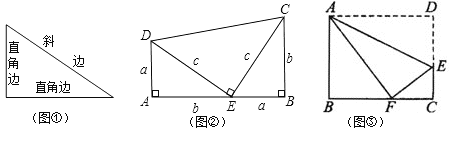
(1)在图②,若![]() ,
,![]() ,则
,则![]() ;
;
(2)观察图②,利用面积与代数恒等式的关系,试说明![]() 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中,每个小正方形的边长都为1,网格中有两个格点![]() 、
、![]() 和直线
和直线![]() ,且
,且![]() 长为3.6.
长为3.6.
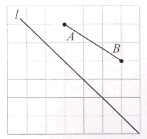
(1)求作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
(2)![]() 为直线
为直线![]() 上一动点,在图中标出使
上一动点,在图中标出使![]() 的值最小的
的值最小的![]() 点,且求出
点,且求出![]() 的最小值?
的最小值?
(3)求![]() 周长的最小值?
周长的最小值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.

(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A= .
(3)当n=60°时,EB=7,BC=12,DC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一记手跑高球,球从地面1.4米的A处抛出(A在y轴上),运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面3.2米高,球落地点为C点.
(1)求足球开始抛出到第一次落地时,该抛物线的解析式.
(2)足球第一次落地点C距守门员多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为![]() ,若AC=4,求图中阴影部分面积S;
,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为半径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D
关AC对称,DF⊥DE于点D,并交EC的延长线与点F.下列结论:①CE=CF;②线段EF的最小值为2![]()
③当AD=2时,EF与半圆相切;④当点D从点A运动到点B时,线段EF扫过的面积是16![]() .其中正
.其中正
确的结论()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图①,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
(2)如图②,若∠ABC=120°,cos∠ADC=![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
(3)如图③,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com