
【题目】如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为![]() ,若AC=4,求图中阴影部分面积S;
,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.

【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)欲证明AB=BC,只要证明∠BAC=∠ACB即可;
(2)设AB的延长线交FG于M,连接CM,在BC上取一点N,使得CN=NM.证明Rt△CBM≌Rt△CGM,可得∠NCM=∠NMC=15°,从而∠MNB=30°,设BM=a,则MN=CN=2a,BN=![]() a,由2a+
a,由2a+![]() a=2
a=2![]() ,可求出BM的长,然后根据三角形面积公式计算即可;
,可求出BM的长,然后根据三角形面积公式计算即可;
(3)连接OB、BF、作FH⊥AC于H.只要证明四边形OBFH是矩形即可解决问题;
(1)证明:如图1中,

∵DA=DB,
∴∠DAB=∠DBA,
∵AE=AB,
∴∠AEB=∠ABE,
∴∠AEB=∠DAB,
∴∠EAD+∠ADE=∠EAD+∠EAB,
∴∠EAB=∠ADE,
∵∠ADE=∠ACB,
∴∠EAB=∠ACB,
∴AB=BC.
(2)如图2中,设AB的延长线交FG于M,连接CM,在BC上取一点N,使得CN=NM.

∵△ABC是等腰直角三角形,AC=4,
∴AB=BC=2![]() ,
,
∵BC=CG,CM=CM,
∴Rt△CBM≌Rt△CGM,
∴∠MCB=∠MCG=15°,
∵NC=NM,
∴∠NCM=∠NMC=15°,
∴∠MNB=30°,设BM=a,则MN=CN=2a,BN=![]() a,
a,
∴2a+![]() a=2
a=2![]() ,
,
∴a=4![]() ﹣2
﹣2![]() ,
,
∴S阴=2×![]() ×BM×BC=(4
×BM×BC=(4![]() ﹣2
﹣2![]() )×
)×![]() =16﹣8
=16﹣8![]() .
.
(3)如图2﹣1中,连接OB、BF、作FH⊥AC于H.

∵∠ACF=30°,∠FHC=90°,
∴FH=![]() CF=
CF=![]() AC=OA=OB,
AC=OA=OB,
∵BA=BC,OA=OC,
∴BO⊥AC,
∴FH∥OB,
∴四边形OBFH是平行四边形,
∵∠BOH=90°,
∴四边形OBFH是矩形,
∴∠OBF=90°,即OB⊥BF;
∴BF是⊙O的切线.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
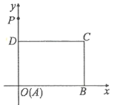
【题目】如图,矩形ABCD在平面直角坐标系的位置如图,A(0,0),B(6,0),D(0,4)
(1) 根据图形直接写出点C的坐标;
(2) 已知直线m经过点P(0,6)且把矩形ABCD分成面积相等的两部分,请只用直尺准确地画出直线m,并求该直线m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.



(1)图2中的阴影部分的面积为 ;
(2)观察图2,三个代数式![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)若![]() ,
,![]() ,求
,求![]() ;
;
(4)观察图3,你能得到怎样的代数恒等式呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
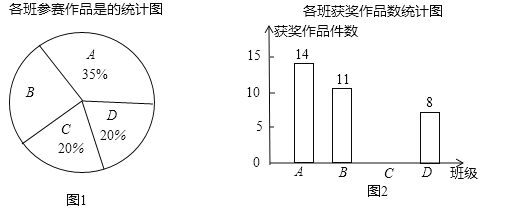
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x+m)2+m与直线y=x相交于E,C两点(点E在点C的左边),抛物线与x轴交
于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
⑴ 若抛物线与y轴交点坐标为(0,2),求m的值;
⑵ 求证:⊙H与直线y=1相切;
⑶ 若DE=2EC,求⊙H的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com