
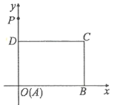
【题目】如图,矩形ABCD在平面直角坐标系的位置如图,A(0,0),B(6,0),D(0,4)
(1) 根据图形直接写出点C的坐标;
(2) 已知直线m经过点P(0,6)且把矩形ABCD分成面积相等的两部分,请只用直尺准确地画出直线m,并求该直线m的解析式.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图所示,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B,C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内,且点A在点D的左侧.
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长p关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么可以用数学语言表达:
,那么可以用数学语言表达:![]() .
.
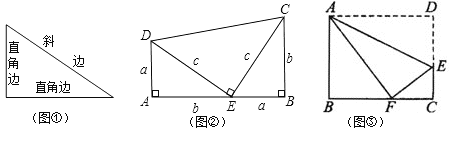
(1)在图②,若![]() ,
,![]() ,则
,则![]() ;
;
(2)观察图②,利用面积与代数恒等式的关系,试说明![]() 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足![]() ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.

(1)∠ABE=15°, ∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为80,BD=16,求E到BC边的距离为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在□ABCD内部,AF∥BE,DF∥CE.

(1)求证:△BCE≌△ADF;
(2)设□ABCD的面积为20,求四边形AEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为![]() ,若AC=4,求图中阴影部分面积S;
,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com