
【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么可以用数学语言表达:
,那么可以用数学语言表达:![]() .
.
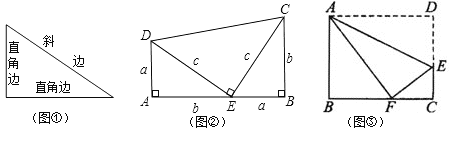
(1)在图②,若![]() ,
,![]() ,则
,则![]() ;
;
(2)观察图②,利用面积与代数恒等式的关系,试说明![]() 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
【答案】(1)12; (2)答案见解析;(3)5
【解析】
试题
(1)利用题中所给公式:![]() ,代入
,代入![]() 即可解出
即可解出![]() 的值;
的值;
(2)先用“梯形面积计算公式”计算出图②的面积,再分别计算图②中三个三角形的面积并相加得到图②的面积,利用两次所求面积相等得到等式,把等式变形即可得到公式:![]() ;
;
(3)由矩形和折叠的性质可得:AF=AD=BC=10,DC=AB=8,EF=DE;在Rt△ABF中,由题中所给结论可计算出BF的长,从而可得FC的长;设EF=![]() ,则DE=
,则DE=![]() ,EC=
,EC=![]() ,这样在Rt△EFC中,由题中所给结论可得关于
,这样在Rt△EFC中,由题中所给结论可得关于![]() 的方程,解方程即可求得EF的长.
的方程,解方程即可求得EF的长.
试题解析:
(1)∵![]() ,代入
,代入![]() ,
,
∴![]() ;
;
(2)∵图①的面积=![]() =
=![]() ,
,
图①的面积=S梯形ABCD=![]() =
=![]() ,
,
∴ ![]() =
=![]() ,
,
∴![]() ,
,
即![]() .
.
(3)由四边形ABCD是矩形和折叠的性质可得,![]() ,
,![]() ,EF=DE,
,EF=DE,
由题意可得:在Rt△ABF中,![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
又∵![]() ,
,
∴ ![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
∵在Rt△ECF中,![]() ,
,
∴![]() ,
,
解得 ![]() ,即
,即![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.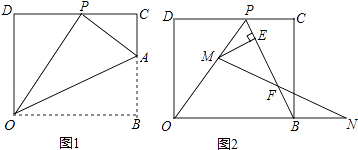
(1)如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(2 ![]() ,2)、B(2
,2)、B(2 ![]() ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2 ![]() ,2
,2 ![]() )的位置,则图中阴影部分的面积为 .
)的位置,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
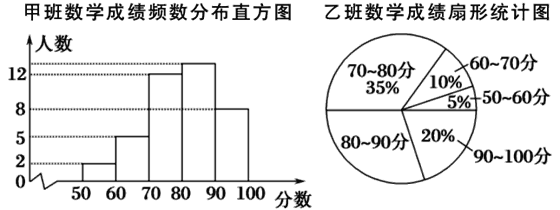
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O是△ABC的外接圆,AB是直径,过 ![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP; 
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG; 
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ![]() ,求AC的长.
,求AC的长. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com