
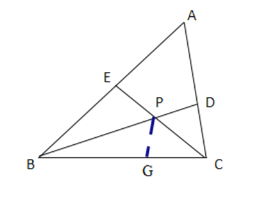
【题目】如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.

(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A= .
(3)当n=60°时,EB=7,BC=12,DC的长为 .
【答案】(1)∠BPC=90°+![]() n,推理过程见解析;(2)70°;(3)5.
n,推理过程见解析;(2)70°;(3)5.
【解析】
(1)根据角平分线的性质得∠ABC=2∠PBC,∠ACB=2∠PCB,再根据三角形内角和定理求得∠A=-180°+2∠BPC,即可求证∠BPC=90°+![]() n;
n;
(2)根据(1)可知∠BPC=90°+![]() n,把∠BPC=125°代入原式求出n即为∠A的度数;
n,把∠BPC=125°代入原式求出n即为∠A的度数;
(3)当n=60°时,即可求出∠BPC=120°,作辅助线在CB上截取CG=CD,可证出△CPG≌△PCD(SAS),即可得出∠DPO=∠GPC,PD=PG,再可证出△BEP≌△BGP,即可得出BE=BG,即可求出DC.
解:(1)∵DB、CE分别为∠ABC,∠ACB的平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB.
∵∠A=180°-(∠ABC+∠ACB),
∴∠A=180°-2(∠PBC+∠PCB),
∴∠A=180°-2(180°-∠BPC),
∴∠A=-180°+2∠BPC,
∴2∠BPC=180°+∠A,
∴∠BPC=90°+![]() ∠A,
∠A,
∴∠BPC=90°+![]() n
n
(2)由(1)知∠BPC=90°+![]() ∠A
∠A
∴当∠BPC=125°时,∠A =2×(125°-90°)= 70°;
(3)在CB上截取CG=CD,连接GP,
![]() CE平分
CE平分![]()
∴∠GCP=∠PCD,
在△PCD和△PCG中,
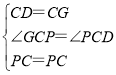
∴△PCD≌△CGP(SAS),
∴∠GPC=∠CPD,PG=PD,
由∠BPG+∠GPC=120°,
又∵∠BPG+2∠GPC=180°,
解得:∠BPG=∠GPC=∠FPC=60°
在△BEP和△BGP中,
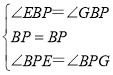
∴△BEP≌△BGP(ASA),
∴BE=BG,
∴CG=BC-BG=BC-BE=12-7=5
∴CD=CG=5.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.

(1)已知点A的坐标为![]() .①在点
.①在点![]()
![]()
![]() 中,为点A的“等距点”的是________;②若点B的坐标为
中,为点A的“等距点”的是________;②若点B的坐标为![]() ,且A,B两点为“等距点”,则点B的坐标为________.
,且A,B两点为“等距点”,则点B的坐标为________.
(2)若![]()
![]() 两点为“等距点”,求k的值.
两点为“等距点”,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB于点E,且△DEA的周长为2019cm,则AB=______.
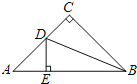
查看答案和解析>>
科目:初中数学 来源: 题型:
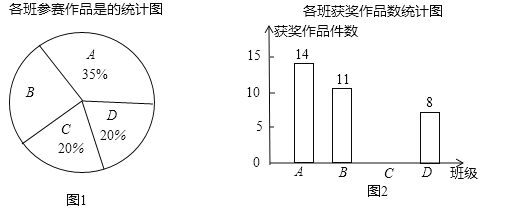
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com