
°æƒø°ø…∆”⁄≤ª∂œ∏ƒΩ¯—ßœ∞∑Ω∑®µƒ–°µœ∑¢œ÷£¨∂‘Ω‚Ã‚Ω¯––ªÿπÀ∑¥Àº£¨—ßœ∞–ßπ˚∏¸∫√£Æƒ≥“ªÃÏ–°µœ”–20∑÷÷” ±º‰ø…”√”⁄—ßœ∞£ÆºŸ…Ë–°µœ”√”⁄Ω‚Ã‚µƒ ±º‰![]() £®µ•Œª£∫∑÷÷”£©”Ηߜ∞ ’“Ê¡ø
£®µ•Œª£∫∑÷÷”£©”Ηߜ∞ ’“Ê¡ø![]() µƒπÿœµ»ÁÕº1À˘ 棨”√”⁄ªÿπÀ∑¥Àºµƒ ±º‰
µƒπÿœµ»ÁÕº1À˘ 棨”√”⁄ªÿπÀ∑¥Àºµƒ ±º‰![]() £®µ•Œª£∫∑÷÷”£©”Ηߜ∞ ’“Ê
£®µ•Œª£∫∑÷÷”£©”Ηߜ∞ ’“Ê![]() µƒπÿœµ»ÁÕº2À˘ 森∆‰÷–
µƒπÿœµ»ÁÕº2À˘ 森∆‰÷–![]() «≈◊ŒÔœþµƒ“ª≤ø∑÷£¨
«≈◊ŒÔœþµƒ“ª≤ø∑÷£¨![]() Œ™≈◊ŒÔœþµƒ∂•µ„£©£¨«“”√”⁄ªÿπÀ∑¥Àºµƒ ±º‰≤ª≥¨π˝”√”⁄Ω‚Ã‚µƒ ±º‰£Æ
Œ™≈◊ŒÔœþµƒ∂•µ„£©£¨«“”√”⁄ªÿπÀ∑¥Àºµƒ ±º‰≤ª≥¨π˝”√”⁄Ω‚Ã‚µƒ ±º‰£Æ
£®1£©«Û–°µœΩ‚µƒ—ßœ∞ ’“Ê¡ø![]() ”Δ√”⁄Ω‚Ã‚µƒ ±º‰
”Δ√”⁄Ω‚Ã‚µƒ ±º‰![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
£®2£©«Û–°µœªÿπÀ∑¥Àºµƒ—ßœ∞ ’“Ê¡ø![]() ”Δ√”⁄ªÿπÀ∑¥Àºµƒ ±º‰
”Δ√”⁄ªÿπÀ∑¥Àºµƒ ±º‰![]() µƒ∫Ø ˝πÿœµ Ω£ª
µƒ∫Ø ˝πÿœµ Ω£ª
£®3£©Œ –°µœ»Á∫Œ∑÷≈‰Ω‚Â∫ÕªÿπÀ∑¥Àºµƒ ±º‰£¨≤≈ƒÐ π’‚20∑÷÷”µƒ—ßœ∞ ’“Ê◊Сø◊Ó¥Û£ø
°æ¥∞∏°øΩ‚£∫£®1£©”…Õº1£¨…Ë![]() £Æµ±
£Æµ±![]() ±£¨
±£¨![]() £¨
£¨
Ω‚µ√![]() £¨
£¨![]() £Æ
£Æ
£®2£©”…Õº2£¨µ±![]() ±£¨…Ë
±£¨…Ë![]() £Æ
£Æ
µ±![]() ±£¨
±£¨![]() £¨
£¨
![]() £Æ
£Æ
![]() £Æ
£Æ
![]() £¨º¥
£¨º¥![]() £Æ
£Æ
µ±![]() ±£¨
±£¨![]() £Æ
£Æ
“Ú¥À![]()
£®3£©…Ë–°µœ”√”⁄ªÿπÀ∑¥Àºµƒ ±º‰Œ™![]() ∑÷÷”£¨
∑÷÷”£¨
—ßœ∞ ’“Ê◊СøŒ™![]() £¨‘ÚÀ˝”√”⁄Ω‚Ã‚µƒ ±º‰Œ™
£¨‘ÚÀ˝”√”⁄Ω‚Ã‚µƒ ±º‰Œ™![]() ∑÷÷”£Æ
∑÷÷”£Æ
µ±![]() ±£¨
±£¨![]() £Æ
£Æ
µ±![]() ±£¨
±£¨![]() £Æ
£Æ
µ±![]() ±£¨
±£¨![]() £Æ
£Æ
![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯ºı–°£¨“Ú¥Àµ±
µƒ‘ˆ¥Û∂¯ºı–°£¨“Ú¥Àµ±![]() ±£¨
±£¨![]() £Æ
£Æ
◊€…œ£¨µ±![]() ±£¨
±£¨![]() £¨¥À ±
£¨¥À ±![]() £Æ
£Æ
¥£∫–°µœ”√”⁄ªÿπÀ∑¥Àºµƒ ±º‰Œ™3∑÷÷”£¨”√”⁄Ω‚Ã‚µƒ ±º‰Œ™17∑÷÷” ±£¨—ßœ∞ ’“Ê◊Сø◊Ó¥Û£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚ø…µ√£¨’‚ «“ª∏ˆ’˝±»¿˝∫Ø ˝£¨…Ë≥ˆ∫Ø ˝πÿœµ Ω£¨‘Ÿ∏˘æ𵄣®1,2£©º¥µ√Ω·π˚£ª
£®2£©’‚ «“ª∏ˆ∑÷∂Œ∫Ø ˝£¨µ⁄“ª∂Œ «∂˛¥Œ∫Ø ˝£¨∏˘æðÕºœÛÃÿ’˜…Ë≥ˆ∂•µ„ Ω£¨‘Ÿ∏˘æðÕºœÛæ≠π˝‘≠µ„º¥µ√Ω‚Œˆ Ω£¨µ⁄∂˛∂Œ «“ª∏ˆ≥£ ˝∫Ø ˝![]() £ª
£ª
∏˘æð°∞—ßœ∞ ’“Ê◊Сø=Ω‚Ã‚µƒ—ßœ∞ ’“Ê¡ø+ªÿπÀ∑¥Àºµƒ—ßœ∞ ’“Ê¡ø°±£¨∑÷±‘⁄![]() º∞
º∞![]() ¡Ω∂Œ ±º‰∑∂Œßƒ⁄µ√µΩ∫Ø ˝πÿœµ Ω£¨‘Ÿ∏˘æð∫Ø ˝Ãÿ’˜º¥ø…µ√µΩΩ·π˚°£
¡Ω∂Œ ±º‰∑∂Œßƒ⁄µ√µΩ∫Ø ˝πÿœµ Ω£¨‘Ÿ∏˘æð∫Ø ˝Ãÿ’˜º¥ø…µ√µΩΩ·π˚°£


 øŒÃ√»´Ω‚◊÷¥ æ‰∂Œ∆™’¬œµ¡–¥∞∏
øŒÃ√»´Ω‚◊÷¥ æ‰∂Œ∆™’¬œµ¡–¥∞∏ ≤Ω≤Ω∏þø⁄À„Âø®œµ¡–¥∞∏
≤Ω≤Ω∏þø⁄À„Âø®œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°˜ABC‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–µƒŒª÷√»ÁÕºÀ˘ æ£Æ

£®1£©ª≠≥ˆ°˜ABCπÿ”⁄y÷·∂‘≥∆µƒ°˜A1B1C1£ª
£®2£©Ω´°˜ABCœÚ”“∆Ω“∆6∏ˆµ•Œª£¨◊˜≥ˆ∆Ω“∆∫Ûµƒ°˜A2B2C2£¨≤¢–¥≥ˆ°˜A2B2C2∏˜∂•µ„µƒ◊¯±Í£ª
£®3£©π€≤Ï°˜A1B1C1∫Õ°˜A2B2C2£¨À¸√« «∑Òπÿ”⁄ƒ≥Ãı÷±œþ∂‘≥∆£ø»Ù «£¨«Î‘⁄Õº…œª≠≥ˆ’‚Ãı∂‘≥∆÷·£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
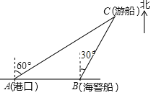
°æƒø°ø“ªÀ“π€π‚”Œ¥¨¥”∏€ø⁄![]() “‘±±∆´∂´
“‘±±∆´∂´![]() µƒ∑ΩœÚ≥ˆ∏€π€π‚£¨∫Ω––
µƒ∑ΩœÚ≥ˆ∏€π€π‚£¨∫Ω––![]() ∫£¿Ô÷¡
∫£¿Ô÷¡![]() ¥¶ ±∑¢…˙¡À≤ý∑≠≥¡¥¨ ¬π £¨¡¢º¥∑¢≥ˆ¡À«Ûæ»–≈∫≈£¨“ªÀ“‘⁄∏€ø⁄’˝∂´∑ΩœÚµƒ∫£æØ¥¨Ω”µΩ«Ûæ»–≈∫≈£¨≤‚µ√ ¬π ¥¨‘⁄À¸µƒ±±∆´∂´
¥¶ ±∑¢…˙¡À≤ý∑≠≥¡¥¨ ¬π £¨¡¢º¥∑¢≥ˆ¡À«Ûæ»–≈∫≈£¨“ªÀ“‘⁄∏€ø⁄’˝∂´∑ΩœÚµƒ∫£æØ¥¨Ω”µΩ«Ûæ»–≈∫≈£¨≤‚µ√ ¬π ¥¨‘⁄À¸µƒ±±∆´∂´![]() ∑ΩœÚ£¨¬Ì…œ“‘
∑ΩœÚ£¨¬Ì…œ“‘![]() ∫£¿Ô√ø–° ±µƒÀŸ∂»«∞Õ˘æ»‘Æ£¨∫£æØ¥¨µΩ¥Ô ¬π ¥¨
∫£¿Ô√ø–° ±µƒÀŸ∂»«∞Õ˘æ»‘Æ£¨∫£æØ¥¨µΩ¥Ô ¬π ¥¨![]() ¥¶À˘–˵ƒ ±º‰¥Û‘ºŒ™________–° ±£®”√∏˘∫≈±Ì 棩£Æ
¥¶À˘–˵ƒ ±º‰¥Û‘ºŒ™________–° ±£®”√∏˘∫≈±Ì 棩£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() °¢
°¢![]() ¡Ωµ„£¨”Î
¡Ωµ„£¨”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() £¨µ„
£¨µ„![]() Œ™≈◊ŒÔœþ…œ“ª∂ص„£¨π˝µ„
Œ™≈◊ŒÔœþ…œ“ª∂ص„£¨π˝µ„![]() ◊˜
◊˜![]() ∆Ω––
∆Ω––![]() Ωª≈◊ŒÔœþ”⁄
Ωª≈◊ŒÔœþ”⁄![]() £¨
£¨![]() °¢
°¢![]() ¡Ωµ„º‰æý¿ÎŒ™
¡Ωµ„º‰æý¿ÎŒ™![]()

![]() «Û
«Û![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
![]() »°œþ∂Œ
»°œþ∂Œ![]() ÷–µ„
÷–µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨µ±
£¨µ±![]() ◊Ó–° ±£¨≈–∂œ“‘µ„
◊Ó–° ±£¨≈–∂œ“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–Œ « ≤√¥Àƒ±þ–Œ£ª
Œ™∂•µ„µƒÀƒ±þ–Œ « ≤√¥Àƒ±þ–Œ£ª
![]() …Ë
…Ë![]() Œ™
Œ™![]() ÷·…œ“ªµ„£¨‘⁄
÷·…œ“ªµ„£¨‘⁄![]() µƒª˘¥°…œ£¨µ±
µƒª˘¥°…œ£¨µ±![]() ±£¨«Ûµ„
±£¨«Ûµ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–Œ![]() ±þ≥§Œ™
±þ≥§Œ™![]() £¨
£¨![]() ÷·£¨
÷·£¨![]() ÷·£¨∂•µ„
÷·£¨∂•µ„![]() «°∫√¬‰‘⁄À´«˙œþ
«°∫√¬‰‘⁄À´«˙œþ![]() …œ£¨±þ
…œ£¨±þ![]() °¢
°¢![]() ∑÷±ΩªÀ´«˙œþ”⁄µ„
∑÷±ΩªÀ´«˙œþ”⁄µ„![]() °¢
°¢![]() £¨»Ùœþ∂Œ
£¨»Ùœþ∂Œ![]() π˝‘≠µ„£¨‘Ú
π˝‘≠µ„£¨‘Ú![]() µƒ√ʪ˝Œ™( )
µƒ√ʪ˝Œ™( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœþy=©Åx2+bx+c…œ≤ø∑÷µ„µƒ∫·◊¯±Íx£¨◊ð◊¯±Íyµƒ∂‘”¶÷µ»Áœ¬±ÌÀ˘ æ£∫
x | °≠ | ©Å2 | ©Å1 | 0 | 1 | 2 | °≠ |
y | °≠ | 0 | 4 | 6 | 6 | 4 | °≠ |
¥”…œ±Ìø…÷™£¨œ¬¡–Àµ∑®÷–£¨¥ÌŒÛµƒ «£® £©
A. ≈◊ŒÔœþ”⁄x÷·µƒ“ª∏ˆΩªµ„◊¯±ÍŒ™£®©Å2£¨0£©
B. ≈◊ŒÔœþ”Îy÷·µƒΩªµ„◊¯±ÍŒ™£®0£¨6£©
C. ≈◊ŒÔœþµƒ∂‘≥∆÷· «÷±œþx=0
D. ≈◊ŒÔœþ‘⁄∂‘≥∆÷·◊Û≤ý≤ø∑÷ «…œ…˝µƒ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨°œBAC=60°„£¨°œBACµƒ∆Ω∑÷œþAD”αþBCµƒ¥π÷±∆Ω∑÷œþMDœýΩª”⁄D£¨DE°ÕABΩªABµƒ—”≥§œþ”⁄E£¨DF°ÕAC£¨œ÷”–œ¬¡–Ω·¬€£∫¢ŸDE=DF£ª ¢⁄DE+DF=AD£ª ¢€DM∆Ω∑÷°œADF£ª ¢ÐAB+AC=2AE,∆‰÷–’˝»∑µƒ∏ˆ ˝”–( )

A.1∏ˆB.2∏ˆC.3∏ˆD.4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨C «AB…œ“ªµ„£¨µ„D£¨E∑÷±‘⁄AB¡Ω≤ý£¨AD°ŒBE£¨«“AD£ΩBC£¨BE£ΩAC£Æ

£®1£©«Û÷§£∫CD£ΩCE£ª
£®2£©¡¨Ω”DE£¨ΩªAB”⁄µ„F£¨≤¬œÎ°˜BEFµƒ–Œ◊¥£¨≤¢∏¯”Ë÷§√˜£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™∂•µ„Œ™£®£≠3£¨£≠6£©µƒ≈◊ŒÔœþ![]() æ≠π˝µ„£®£≠1£¨£≠4£©£¨œ¬¡–Ω·¬€£∫¢Ÿb2£æ4ac£ª¢⁄ax2+bx+c°ð£≠6£ª¢€»Ùµ„£®£≠2£¨m£©£¨£®£≠5£¨n£©‘⁄≈◊ŒÔœþ…œ£¨‘Úm£æn£ª¢Ðπÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ã
æ≠π˝µ„£®£≠1£¨£≠4£©£¨œ¬¡–Ω·¬€£∫¢Ÿb2£æ4ac£ª¢⁄ax2+bx+c°ð£≠6£ª¢€»Ùµ„£®£≠2£¨m£©£¨£®£≠5£¨n£©‘⁄≈◊ŒÔœþ…œ£¨‘Úm£æn£ª¢Ðπÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ã![]() µƒ¡Ω∏˘Œ™©Å5∫Õ©Å1£¨∆‰÷–’˝»∑µƒ”–£® £©
µƒ¡Ω∏˘Œ™©Å5∫Õ©Å1£¨∆‰÷–’˝»∑µƒ”–£® £©

A. 1∏ˆ B. 2∏ˆ C. 3∏ˆ D. 4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com