
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,点
,点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 平行
平行![]() 交抛物线于
交抛物线于![]() ,
,![]() 、
、![]() 两点间距离为
两点间距离为![]()

![]() 求
求![]() 的解析式;
的解析式;
![]() 取线段
取线段![]() 中点
中点![]() ,连接
,连接![]() ,当
,当![]() 最小时,判断以点
最小时,判断以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是什么四边形;
为顶点的四边形是什么四边形;
![]() 设
设![]() 为
为![]() 轴上一点,在
轴上一点,在![]() 的基础上,当
的基础上,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1) 直线![]() 解析式为
解析式为![]() (2) 四边形
(2) 四边形![]() 是菱形,理由见解析;(3)点
是菱形,理由见解析;(3)点![]() 的坐标为
的坐标为![]() 和
和![]()
【解析】
(1)先求得点A、B、C的坐标,再用待定系数法求出直线BC解析式即可;
(2)根据m最小时,直线PQ和抛物线只有一个交点,设直线![]() 解析式
解析式![]() 由直线PQ和抛物线只有一个交点,联立解析式可得
由直线PQ和抛物线只有一个交点,联立解析式可得![]() ,根据△=0求得b值,即可求得直线
,根据△=0求得b值,即可求得直线![]() 解析式及点P的坐标,再利用两点间的距离公式得出BM=OP=OM,即可判断出四边形POMB是菱形;(3)确定出直线PQ解析式,分点
解析式及点P的坐标,再利用两点间的距离公式得出BM=OP=OM,即可判断出四边形POMB是菱形;(3)确定出直线PQ解析式,分点![]() 在
在![]() 轴负半轴上和
轴负半轴上和
点![]() 在
在![]() 轴正半轴两种情况求点N的坐标.
轴正半轴两种情况求点N的坐标.
![]() ∵抛物线
∵抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,
,
∴![]() ,
,
令![]() ,则
,则![]() ,∴
,∴![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,
理由:如图,
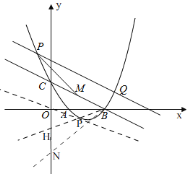
∵![]() 、
、![]() 两点间距离为
两点间距离为![]() ,且
,且![]() 最小,即:
最小,即:![]() ,此时直线
,此时直线![]() 和抛物线只有一个交点,
和抛物线只有一个交点,
∵![]() 平行
平行![]() ,
,
∴设直线![]() 解析式
解析式![]() ①,
①,
∵![]() ②,
②,
联立①②得,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,![]() ,
,
∴直线![]() 过原点,
过原点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,取线段
,取线段![]() 中点
中点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴平行四边形![]() 是菱形;
是菱形;
![]() 由
由![]() 知,
知,![]() ,
,![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
∴![]()
①当点![]() 在
在![]() 轴负半轴上时,
轴负半轴上时,
∵![]() ,
,
∴![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() (舍)或
(舍)或![]() ,
,
∴![]() ,
,
②当点![]() 在
在![]() 轴正半轴时,由对称性得出,
轴正半轴时,由对称性得出,![]()
即点![]() 的坐标为
的坐标为![]() 和
和![]() .
.


科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位祖籍江宁的台商,应区政府的邀请,到科学园考察投资环境.他驱车在东西走向的天元路上由西向东缓慢地前进着,车载![]() (全球卫星定位系统)显示,方山风景区(点
(全球卫星定位系统)显示,方山风景区(点![]() )在其(点
)在其(点![]() )南偏东
)南偏东![]() 的方向上,
的方向上,![]() .他继续向东前进到点
.他继续向东前进到点![]() 的位置,发现方山风景区在其南偏西
的位置,发现方山风景区在其南偏西![]() 的方向上.试求该台商由西向东前进的路程
的方向上.试求该台商由西向东前进的路程![]() 是多少千米?(结果精确到
是多少千米?(结果精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为矩形,AD=20cm、AB=10cm.M点从D到A,P点从B到C,两点的速度都为2cm/s;N点从A到B,Q点从C到D,两点的速度都为1cm/s.若四个点同时出发.
(1)判断四边形MNPQ的形状.
(2)四边形MNPQ能为菱形吗?若能,请求出此时运动的时间;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间![]() (单位:分钟)与学习收益量
(单位:分钟)与学习收益量![]() 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间![]() (单位:分钟)与学习收益
(单位:分钟)与学习收益![]() 的关系如图2所示(其中
的关系如图2所示(其中![]() 是抛物线的一部分,
是抛物线的一部分,![]() 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量![]() 与用于解题的时间
与用于解题的时间![]() 之间的函数关系式;
之间的函数关系式;
(2)求小迪回顾反思的学习收益量![]() 与用于回顾反思的时间
与用于回顾反思的时间![]() 的函数关系式;
的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() 是抛物线的顶点,三角形
是抛物线的顶点,三角形![]() 的面积等于
的面积等于![]() ,则下列结论:
,则下列结论:
①![]() ②
②![]() ③
③![]() ④
④![]()
其中正确的结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com