
����Ŀ��ij���ڵ�����ʵʩ������ƶ�����ߵĺ����£�������չ�Ƽ���ƶ����������ũ���齨ũ����Ʒ���۹�˾��ijũ����Ʒ�������������100������ò�Ʒ����������y����Ԫ���������x�������֮��ĺ���ͼ���Ƕ���Ϊԭ��������ߵ�һ���֣���ͼ����ʾ�����ò�Ʒ�����۵���z��Ԫ/��������������x�������֮��ĺ���ͼ������ͼ����ʾ��һ���߶Σ��������IJ�Ʒ�����ڵ��������꣬�ﵽ����ƽ�⣬����ë����Ϊw��Ԫ����ë����=���۶�������ã�

��1����ֱ��д��y��x�Լ�z��x֮��ĺ�����ϵʽ��
��2����w��x֮��ĺ�����ϵʽ������������������ʱ������ë����������ë�����Ƕ��٣�
��3���������ʽ��Ӱ�죬����Ͷ�������ķ��ò��ᳬ��360��Ԫ���������ɻ�ö�����Ԫ��ë����
���𰸡���1��y=![]() x2��z=��
x2��z=��![]() x+30����2��W==��
x+30����2��W==��![]() x2+30x�������Ϊ75���ʱë����������ë����Ϊ1125��Ԫ����3���������ɻ��1080��Ԫ��ë����.
x2+30x�������Ϊ75���ʱë����������ë����Ϊ1125��Ԫ����3���������ɻ��1080��Ԫ��ë����.
��������
��1�����ͼ�����ô���ϵ�������y��x�Լ�z��x֮��ĺ�����ϵʽ��������2������ë����=���۶�������ÿɵ�w��x֮��ĺ�����ϵʽ�������ö��κ�����������⼴�ɣ���3����y=0���ⷽ�����x��ֵ������ͼ����y��ȡֵ��Χ�����x��ȡֵ��Χ�����ɶ��κ��������ʼ��ɽ��.
��1��ͼ�ٿɵú��������㣨100��1000����
�������ߵĽ���ʽΪy=ax2��a��0����
���㣨100��1000������ã�1000=10000a��
��ã�a=![]() ��
��
��y��x֮��Ĺ�ϵʽΪy=![]() x2��
x2��
ͼ�ڿɵã����������㣨0��30������100��20����
��z=kx+b����![]() ��
��
��ã�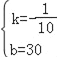 ��
��
��z��x֮��Ĺ�ϵʽΪz=��![]() x+30��
x+30��
��2��W=zx��y=��![]() x2+30x��
x2+30x��![]() x2
x2
=��![]() x2+30x
x2+30x
=��![]() ��x2��150x��
��x2��150x��
=��![]() ��x��75��2+1125��
��x��75��2+1125��
����![]() ��0��
��0��
�൱x=75ʱ��W�����ֵ1125��
�������Ϊ75���ʱë����������ë����Ϊ1125��Ԫ��
��3����y=360����![]() x2=360��
x2=360��
��ã�x=��60����ֵ��ȥ����
��ͼ���֪����0��y��360ʱ��0��x��60��
��W=��![]() ��x��75��2+1125�����ʿ�֪��
��x��75��2+1125�����ʿ�֪��
��0��x��60ʱ��W��x�����������
�ʵ�x=60ʱ��W�����ֵ1080��
�𣺽������ɻ��ë����1080��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
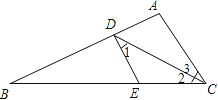
����Ŀ����ͼ����֪CDƽ�֡�ACB����1=��2��
��1����֤��DE��AC��
��2������3=30������B=25�������BDE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ʵ��ڵ�һ����x�ᡢy�����˶�����ÿ���ƶ�һ����λ���ڵ�1���ӣ�����ԭ���˶�����0��1����Ȼ����Ű�ͼ�м�ͷ��ʾ�����˶�������0��0������0��1������1��1������1��0��������������23���ʵ㵽���A������33���ʵ㵽���B����ֱ��AB�Ľ���ʽΪ�� ��

A.y��![]() x+
x+![]() B.y����
B.y����![]() x+
x+![]() C.y��2x+9D.y����2x+9
C.y��2x+9D.y����2x+9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
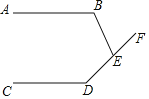
����Ŀ����ͼ��AB��CD��BE��DF�ཻ�ڵ�E��
��1������B��110������D��145�������BEF�Ķ�����
��2�������B����D����BEF֮��Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������仯�����Ѿ�����������ĸ߶ȹ�ע���йز�����ȫ����Χ�ڶ�12��35��������Ⱥ�����˼�����������飬���Ƴ���������ͳ��ͼ��

�����ͼ�е���Ϣ���ش��������⣺
��1����γ��������й������������ˣ�
��2���벹ȫ����ͳ��ͼ��
��3������ͳ��ͼ��18��23�겿�ֵ�Բ�ĽǵĶ�����������
��4���ݱ�����Ŀǰ�ҹ�12��35���������ԼΪ2000�����������12��23�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��

��1��������ABC����y��ԳƵġ�A1B1C1��
��2������ABC����ƽ��6����λ������ƽ�ƺ�ġ�A2B2C2����д����A2B2C2����������ꣻ
��3���۲��A1B1C1�͡�A2B2C2�������Ƿ����ij��ֱ�߶Գƣ����ǣ�����ͼ�ϻ��������Գ��ᣮ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ѧ��쳲��������о����ӷ�ֳ����ʱ������������һ������1��1��2��3��5��8��13���������дӵ���������ÿһ������������ǰ���������ĺ��������������еĸ�������Ϊ�����εı߳�ֵ���������Σ��ٷֱ����δ�����ȡ2����3����4����5����������ƴ�����ϳ����Σ������˹��ɼ����������Σ������Ϊ���ij������ܳ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() ����
����![]() Ϊ��������һ���㣬����
Ϊ��������һ���㣬����![]() ��
��![]() ƽ��
ƽ��![]() ����������
����������![]() ��
��![]() ��
��![]() ��������Ϊ
��������Ϊ![]()

![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() ȡ�߶�
ȡ�߶�![]() �е�
�е�![]() ������
������![]() ����
����![]() ��Сʱ���ж��Ե�
��Сʱ���ж��Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ʲô�ı��Σ�
Ϊ������ı�����ʲô�ı��Σ�
![]() ��
��![]() Ϊ
Ϊ![]() ����һ�㣬��
����һ�㣬��![]() �Ļ����ϣ���
�Ļ����ϣ���![]() ʱ�����
ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com