
【题目】如图,![]() 的
的![]() 、
、![]() 的平分线
的平分线![]() 、
、![]() 相交于点
相交于点![]() ,求证:
,求证:![]() .
.
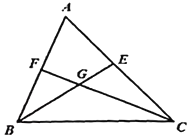
【答案】见解析
【解析】
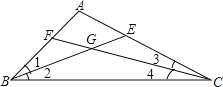
先根据△ABC的∠B和∠C的平分线BE,CF交于点G得出∠1=∠2=![]() ∠ABC,∠3=∠4=
∠ABC,∠3=∠4=![]() ∠ACB,再由三角形内角和定理得出∠ABC+∠ACB=180°-∠A,进而可得出∠2+∠4=90°-
∠ACB,再由三角形内角和定理得出∠ABC+∠ACB=180°-∠A,进而可得出∠2+∠4=90°-![]() ∠A,由∠BGC+(∠2+∠4)=180°即可得出结论.
∠A,由∠BGC+(∠2+∠4)=180°即可得出结论.
∵△ABC的∠B和∠C的平分线BE,CF交于点G,
∴∠1=∠2=![]() ∠ABC,∠3=∠4=
∠ABC,∠3=∠4=![]() ∠ACB,
∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴![]() (∠ABC+∠ACB)=90°-
(∠ABC+∠ACB)=90°-![]() ∠A,即∠2+∠4=90°-
∠A,即∠2+∠4=90°-![]() ∠A,
∠A,
∵∠BGC+(∠2+∠4)=180°,
∴∠BGC=180°-(∠2+∠4)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A.
∠A.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,4),B(8,0),C(8,4),连接AC,BC得到四边形AOBC,点D在边AC上,连接OD,将边OA沿OD折叠,点A的对应点为点P,若点P到四边形AOBC较长两边的距离之比为1:3,则点P的坐标为__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步促进“美丽校园”创建工作,某校团委计划对八年级五个班的文化建设进行检查,每天随机抽查一个班级,第一天从五个班级随机抽取一个进行检查,第二天从剩余的四个班级再随机抽取一个进行检查,第三天从剩余的三个班级再随机抽取一个进行检查…,以此类推,直到检查完五个班级为止,且每个班级被选中的机会均等
(1)第一天,八(1)班没有被选中的概率是 ;
(2)利用网状图或列表的方法,求前两天八(1)班被选中的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
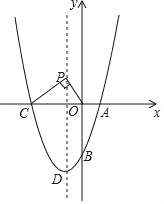
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、C两点,点A在点C的右边,与y轴交于点B,点B的坐标为(0,﹣3),且OB=OC,点D为该二次函数图象的顶点.
(1)求这个二次函数的解析式及顶点D的坐标;
(2)如图,若点P为该二次函数的对称轴上的一点,连接PC、PO,使得∠CPO=90°,请求出所有符合题意的点P的坐标;
(3)在对称轴上是否存在一点P,使得∠OPC为钝角,若存在,请直接写出点P的纵坐标为yp的取值范围,若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com