
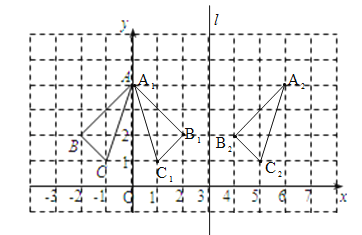
【题目】△ABC在平面直角坐标系中的位置如图所示.

(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
【答案】(1)见解析;(2)见解析,A2(6,4),B2(4,2),C2(5,1);(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3,见解析.
【解析】
(1)根据轴对称图形的性质,找出A、B、C的对称点A1、B1、C1,画出图形即可;
(2)根据平移的性质,△ABC向右平移6个单位,A、B、C三点的横坐标加6,纵坐标不变;
(3)根据轴对称图形的性质和顶点坐标,可得其对称轴是l:x=3.
(1)由图知,A(0,4),B(﹣2,2),C(﹣1,1),∴点A、B、C关于y轴对称的对称点为A1(0,4)、B1(2,2)、C1(1,1),连接A1B1,A1C1,B1C1,得△A1B1C1;
(2)∵△ABC向右平移6个单位,∴A、B、C三点的横坐标加6,纵坐标不变,作出△A2B2C2,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
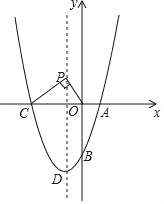
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、C两点,点A在点C的右边,与y轴交于点B,点B的坐标为(0,﹣3),且OB=OC,点D为该二次函数图象的顶点.
(1)求这个二次函数的解析式及顶点D的坐标;
(2)如图,若点P为该二次函数的对称轴上的一点,连接PC、PO,使得∠CPO=90°,请求出所有符合题意的点P的坐标;
(3)在对称轴上是否存在一点P,使得∠OPC为钝角,若存在,请直接写出点P的纵坐标为yp的取值范围,若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.请您确定当购买A种奖品多少件时,费用W的值最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间![]() (单位:分钟)与学习收益量
(单位:分钟)与学习收益量![]() 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间![]() (单位:分钟)与学习收益
(单位:分钟)与学习收益![]() 的关系如图2所示(其中
的关系如图2所示(其中![]() 是抛物线的一部分,
是抛物线的一部分,![]() 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量![]() 与用于解题的时间
与用于解题的时间![]() 之间的函数关系式;
之间的函数关系式;
(2)求小迪回顾反思的学习收益量![]() 与用于回顾反思的时间
与用于回顾反思的时间![]() 的函数关系式;
的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com