
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.

【答案】y=﹣2x+4或y=﹣![]() x+
x+![]()
【解析】∵矩形OABC的顶点B的坐标是(4,2),E是矩形ABCD的对称中心,
∴点E的坐标为(2,1),
代入反比例函数解析式得, ![]() =1,
=1,
解得k=2,
∴反比例函数解析式为y=![]() ,
,
∵点D在边BC上,
∴点D的纵坐标为2,
∴y=2时, ![]() =2,
=2,
解得x=1,
∴点D的坐标为(1,2);如图,设直线与x轴的交点为F,
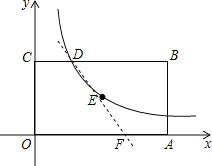
矩形OABC的面积=4×2=8,
∵矩形OABC的面积分成3:5的两部分,
∴梯形OFDC的面积为![]() =3或
=3或![]() ×8=5.
×8=5.
∵点D的坐标为(1,2),
∴若![]() (1+OF)×2=3,
(1+OF)×2=3,
解得OF=2,
此时点F的坐标为(2,0),
则![]() ,
,
解得![]() ,
,
此时,直线解析式为y=-2x+4;
若![]() (1+OF)×2=5,
(1+OF)×2=5,
解得OF=4,
此时点F的坐标为(4,0),与点A重合,
则![]() ,
,
解得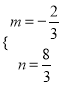 ,
,
此时,直线解析式为![]() ,
,
综上所述,直线的解析式为y=-2x+4或![]() .
.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)当AM的值为 时,四边形AMDN是矩形,请你把猜想出的AM值作为已知条件,说明四边形AMDN是矩形的理由.
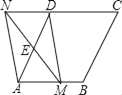
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C路程y(千米)与甲车出发时间t(小时)的关系图象如图所示,则下列说法:①A、B两地之间的距离为180千米;②乙车的速度为36千米/小时;③a=3.75;④当乙车到达终点时,甲车距离终点还有30千米.其中正确的结论有( )
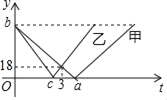
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,已知甲工程队铺设每天需支付工程费2000元,乙工程队铺设每天需支付工程费1500元.
(1)甲、乙两队合作施工多少天能完成该管线的铺设?
(2)由两队合作完成该管线铺设工程共需支付工程费多少元?
(3)根据实际情况,若该工程要求10天完成,从节约资金的角度应怎样安排施工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式![]() x2y4的次数为c.
x2y4的次数为c.
![]()
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明同学早上骑自行车上学,中途因道路施工需步行一段路,到学校共用时18分钟,他骑自行车的平均速度是300米/分钟,步行的平均速度是120米/分钟,他家离学校的距离是4500米.
(1)李明上学时骑自行车的路程和步行的路程分别为多少米?
(2)放学后李明从17:40开始离校回家,但此时道路施工的地段增长了600米,如果按照上学时的速度,问李明能否在18:00之前到家?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A. 8 B. 6 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
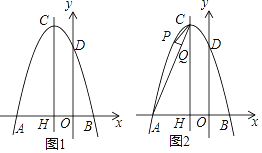
(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com