
【题目】“壮丽70载,奋进新时代”.值伟大祖国70华诞之际,某网店特别推出甲、乙两种纪念文化衫,已知甲种纪念文化衫的售价比乙种纪念文化衫多15元,广益中学陈老师从该网店购买了2件甲种纪念文化衫和3件乙种纪念文化衫,共花费255元.
(1)该网店甲、乙两种纪念文化衫每件的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种纪念文化衫共200件,且甲种纪念文化衫的数量大于乙种纪念文化衫数量的![]() ,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
①若设购进甲种纪念文化衫m件,则该网店有哪几种进货方案?
②若所购进纪念文化衫均可全部售出,请求出网店所获利润W(元)与甲种纪念文化衫进货量m(件)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
【答案】(1)甲种纪念文化衫每件的售价是60元,乙种纪念文化衫每件的售价是45元;(2)①进货方案有三种,分别为:方案一:购进甲种纪念文化衫76件,则乙种纪念文化衫为124件;方案二:购进甲种纪念文化衫77件,则乙种纪念文化衫为123件;方案三:购进甲种纪念文化衫78件,则乙种纪念文化衫为122件;②W=5m+1000,当m=78时,所获利润最大,最大利润为1390元.
【解析】
(1)设甲种纪念文化衫每件的售价是x元,乙种纪念文化衫每件的售价是y元,由题意,列二元一次方程组,求解即可;(2)①若购进甲种纪念文化衫m件,则乙种纪念文化衫为(200m)件,由题意得一元一次不等式组,求解,并根据m为整数,可求得m的值,即可得进货方案;②用含m的式子表示出W,根据一次函数的性质可得答案.
解:(1)设甲种纪念文化衫每件的售价是x元,乙种纪念文化衫每件的售价是y元,由题意得:
![]()
解得:![]()
答:甲种纪念文化衫每件的售价是60元,乙种纪念文化衫每件的售价是45元.
(2)①若购进甲种纪念文化衫m件,则乙种纪念文化衫为(200﹣m)件,
由题意得:
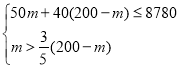
解得:75<m≤78
∵m为整数
∴m的值为:76,77,78.
进货方案有三种,分别为:
方案一:购进甲种纪念文化衫76件,则乙种纪念文化衫为124件;
方案二:购进甲种纪念文化衫77件,则乙种纪念文化衫为123件;
方案三:购进甲种纪念文化衫78件,则乙种纪念文化衫为122件.
②由题意得:
W=(60﹣50)m+(45﹣40)(200﹣m)=5m+1000
∵5>0
∴W随m的增大而增大,且75<m≤78
∴当m=78时,W最大,W的最大值为:5×78+1000=1390元.
答:②当m=78时,所获利润最大,最大利润为1390元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点.
两点.
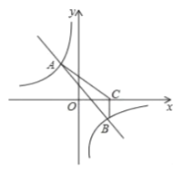
(1)求一次函数与反比例函数的解析式;
(2)根据已知条件,请直接写出不等式![]() 的解集;
的解集;
(3)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为_____m(结果保留根号).
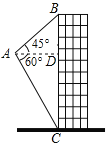
查看答案和解析>>
科目:初中数学 来源: 题型:
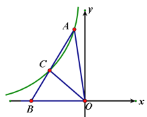
【题目】如图,在△AOB中,OC平分∠AOB,![]() ,反比例函数
,反比例函数![]() 图像经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为( )
图像经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
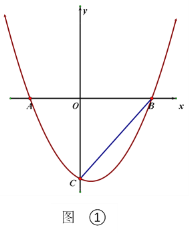
【题目】如图,抛物线![]() 交x轴于A、B两点(点A在点B的左侧),
交x轴于A、B两点(点A在点B的左侧),![]() .
.
(1)求抛物线的函数表达式;
(2)如图①,连接BC,点P在抛物线上,且∠BCO=![]() ∠PBA.求点P的坐标
∠PBA.求点P的坐标
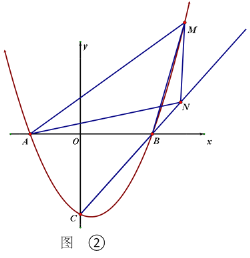
(3)如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,![]() ,点M到
,点M到![]() 轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点 A 是直线 l 上的一点.
求作:正方形 ABCD,使得点 B 在直线 l 上.(要求保留作图痕迹,不用写作法) 请你说明,∠BAD=90°的依据是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
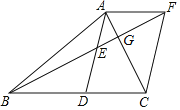
(1)求证:![]() ;
;
(2)若![]() ,①试判断四边形
,①试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
②若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长_________.
的长_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com