
ΓΨΧβΡΩΓΩΈΣ≥ΪΒΦΫΎΡήΜΖ±ΘΘ§ΫΒΒΆΡή‘¥œϊΚΡΘ§Χα≥ΪΜΖ±Θ–Ά–¬Ρή‘¥ΩΣΖΔΘ§‘λΗΘ…γΜαΘ°Ρ≥ΙΪΥΨ―–ΖΔ…ζ≤ζ“Μ÷÷–¬–Ά÷«ΡήΜΖ±ΘΫΎΡήΒΤΘ§≥…±ΨΈΣΟΩΦΰ40‘ΣΘ° –≥ΓΒς≤ιΖΔœ÷Θ§ΗΟ÷«ΡήΜΖ±ΘΫΎΡήΒΤΟΩΦΰ έΦέyΘ®‘ΣΘ©”κΟΩΧλΒΡœζ έΝΩΈΣxΘ®ΦΰΘ©ΒΡΙΊœΒ»γΆΦΘ§ΈΣΆΤΙψ–¬≤ζΤΖΘ§ΙΪΥΨ“Σ«σΟΩΧλΒΡœζ έΝΩ≤Μ…Ό”Ύ1000ΦΰΘ§ΟΩΦΰάϊ»σ≤ΜΒΆ”Ύ5‘ΣΘ°
Θ®1Θ©«σΟΩΦΰœζ έΒΞΦέyΘ®‘ΣΘ©”κΟΩΧλΒΡœζ έΝΩΈΣxΘ®ΦΰΘ©ΒΡΚ· ΐΙΊœΒ Ϋ≤Δ÷±Ϋ”–¥≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©…ηΗΟΙΪΥΨ»’œζ έάϊ»σΈΣP‘ΣΘ§«σΟΩΧλΒΡΉν¥σœζ έάϊ»σ «Εύ…Ό‘ΣΘΩ
Θ®3Θ©‘Ύ ‘œζ έΙΐ≥Χ÷–Θ§ ήΙζΦ“’ΰ≤ΏΖω≥÷Θ§öΑœζ έ“ΜΦΰΗΟ÷«ΡήΜΖ±ΘΫΎΡήΒΤΙζΦ“Ηχ”ηΙΪΥΨ≤ΙΧυmΘ®mΓή40Θ©‘ΣΘ°‘ΎΜώΒΟΙζΦ“ΟΩΦΰm‘Σ≤ΙΧυΚσΘ§ΙΪΥΨΒΡ»’œζ έάϊ»σΥφ»’œζ έΝΩΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρmΒΡ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ®÷±Ϋ”–¥≥ωΫαΙϊΘ©Θ°

ΓΨ¥πΑΗΓΩΘ®1Θ©Κ· ΐΙΊœΒ ΫΈΣyΘΫ©¹![]() x+70Θ§Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß1000ΓήxΓή2500ΘΜΘ®2Θ©ΟΩΧλΒΡΉν¥σœζ έάϊ»σ «22500‘ΣΘΜΘ®3Θ©mΒΡ»Γ÷ΒΖΕΈß «ΘΚ20ΓήmΓή40Θ°
x+70Θ§Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß1000ΓήxΓή2500ΘΜΘ®2Θ©ΟΩΧλΒΡΉν¥σœζ έάϊ»σ «22500‘ΣΘΜΘ®3Θ©mΒΡ»Γ÷ΒΖΕΈß «ΘΚ20ΓήmΓή40Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®2Θ©ΙΙΫ®Εΰ¥ΈΚ· ΐΘ§άϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©ΙΙΫ®Εΰ¥ΈΚ· ΐΘ§άϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Φ¥Ω…ΫβΨωΈ ΧβΘΜ
ΫβΘΚΘ®1Θ©…ηΟΩΦΰœζ έΒΞΦέyΘ®‘ΣΘ©”κΟΩΧλΒΡœζ έΝΩΈΣxΘ®ΦΰΘ©ΒΡΚ· ΐΙΊœΒ ΫΈΣyΘΫkx+bΘ§
Α―Θ®1500Θ§55Θ©”κΘ®2000Θ§50Θ©¥ζ»κyΘΫkx+bΒΟΘ§
![]() Θ§
Θ§
ΫβΒΟΘΚ Θ§
Θ§
ΓύΟΩΦΰœζ έΒΞΦέyΘ®‘ΣΘ©”κΟΩΧλΒΡœζ έΝΩΈΣxΘ®ΦΰΘ©ΒΡΚ· ΐΙΊœΒ ΫΈΣyΘΫ©¹![]() x+70Θ§
x+70Θ§
Β±yΓί45 ±Θ§©¹![]() x+70Γί45Θ§ΫβΒΟΘΚxΓή2500Θ§
x+70Γί45Θ§ΫβΒΟΘΚxΓή2500Θ§
ΓύΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß1000ΓήxΓή2500ΘΜ
Θ®2Θ©ΗυΨίΧβ“βΒΟΘ§PΘΫΘ®y©¹40Θ©xΘΫΘ®©¹![]() x+70©¹40Θ©xΘΫ©¹
x+70©¹40Θ©xΘΫ©¹![]() x2+30xΘΫ©¹
x2+30xΘΫ©¹![]() Θ®x©¹1500Θ©2+22500Θ§
Θ®x©¹1500Θ©2+22500Θ§
ΓΏ©¹![]() ΘΦ0Θ§P”–Ήν¥σ÷ΒΘ§
ΘΦ0Θ§P”–Ήν¥σ÷ΒΘ§
Β±xΘΦ1500 ±Θ§PΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΓύΒ±xΘΫ1500 ±Θ§PΒΡΉν¥σ÷ΒΈΣ22500‘ΣΘ§
¥πΘΚΟΩΧλΒΡΉν¥σœζ έάϊ»σ «22500‘ΣΘΜ
Θ®3Θ©”…Χβ“βΒΟΘ§PΘΫΘ®©¹![]() x+70©¹40+mΘ©xΘΫ©¹
x+70©¹40+mΘ©xΘΫ©¹![]() x2+Θ®30+mΘ©xΘ§
x2+Ȯ30+mȩxȧ
ΓΏΕ‘≥Τ÷αΈΣxΘΫ50Θ®30+mΘ©Θ§
ΓΏ1000ΓήxΓή2500Θ§
ΓύxΒΡ»Γ÷ΒΖΕΈß‘ΎΕ‘≥Τ÷αΒΡΉσ≤ύ ±PΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§
50Θ®30+mΘ©Γί2500Θ§
ΫβΒΟΘΚmΓί20Θ§
ΓύmΒΡ»Γ÷ΒΖΕΈß «ΘΚ20ΓήmΓή40Θ°
Ι ¥πΑΗΈΣΘΚ20ΓήmΓή40Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑΉ≥άω70‘ΊΘ§ΖήΫχ–¬ ±¥ζΓ±Θ°÷ΒΈΑ¥σΉφΙζ70ΜΣΒ°÷°Φ Θ§Ρ≥ΆχΒξΧΊ±πΆΤ≥ωΦΉΓΔ““ΝΫ÷÷ΦΆΡνΈΡΜ·…άΘ§“―÷ΣΦΉ÷÷ΦΆΡνΈΡΜ·…άΒΡ έΦέ±»““÷÷ΦΆΡνΈΡΜ·…άΕύ15‘ΣΘ§Ιψ“φ÷–―ß≥¬άœ Π¥”ΗΟΆχΒξΙΚ¬ρΝΥ2ΦΰΦΉ÷÷ΦΆΡνΈΡΜ·…άΚΆ3Φΰ““÷÷ΦΆΡνΈΡΜ·…άΘ§Ι≤Μ®Ζ―255‘ΣΘ°
Θ®1Θ©ΗΟΆχΒξΦΉΓΔ““ΝΫ÷÷ΦΆΡνΈΡΜ·…άΟΩΦΰΒΡ έΦέΗς «Εύ…Ό‘ΣΘΩ
Θ®2Θ©ΗυΨίœϊΖ―’Ώ–η«σΘ§ΗΟΆχΒξΨωΕ®”Ο≤Μ≥§Ιΐ8780‘ΣΙΚΫχΦΉΓΔ““ΝΫ÷÷ΦΆΡνΈΡΜ·…άΙ≤200ΦΰΘ§«“ΦΉ÷÷ΦΆΡνΈΡΜ·…άΒΡ ΐΝΩ¥σ”Ύ““÷÷ΦΆΡνΈΡΜ·…ά ΐΝΩΒΡ![]() Θ§“―÷ΣΦΉ÷÷ΦΆΡνΈΡΜ·…άΟΩΦΰΒΡΫχΦέΈΣ50‘ΣΘ§““÷÷ΦΆΡνΈΡΜ·…άΟΩΦΰΒΡΫχΦέΈΣ40‘ΣΘ°
Θ§“―÷ΣΦΉ÷÷ΦΆΡνΈΡΜ·…άΟΩΦΰΒΡΫχΦέΈΣ50‘ΣΘ§““÷÷ΦΆΡνΈΡΜ·…άΟΩΦΰΒΡΫχΦέΈΣ40‘ΣΘ°
ΔΌ»τ…ηΙΚΫχΦΉ÷÷ΦΆΡνΈΡΜ·…άmΦΰΘ§‘ρΗΟΆχΒξ”–ΡΡΦΗ÷÷ΫχΜθΖΫΑΗΘΩ
ΔΎ»τΥυΙΚΫχΦΆΡνΈΡΜ·…άΨυΩ…»Ϊ≤Ω έ≥ωΘ§«κ«σ≥ωΆχΒξΥυΜώάϊ»σWΘ®‘ΣΘ©”κΦΉ÷÷ΦΆΡνΈΡΜ·…άΫχΜθΝΩmΘ®ΦΰΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤ΔΥΒΟςΒ±mΈΣΚΈ÷Β ±ΥυΜώάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ°ΒψEΘ§FΖ÷±π‘ΎBCΘ§CD…œΘ§ΓςAEF «Β»±Ώ»ΐΫ«–ΈΘ°Ν§Ϋ”ACΫΜEF”ΎΒψGΘ°ΙΐΒψGΉςGHΓΆCE”ΎΒψHΘ°»τ![]() Θ§‘ρ
Θ§‘ρ![]() =Θ®ΓΓΓΓΘ©
=Θ®ΓΓΓΓΘ©

A. 6 B. 4 C. 3 D. 2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
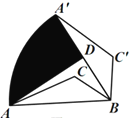
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§AB=4Θ§»τΫΪΓςABC»ΤΒψBΥ≥ ±’κ–ΐΉΣ60ΓψΘ§ΒψAΒΡΕ‘”ΠΒψΈΣΒψAΓδΘ§ΒψCΒΡΕ‘”ΠΒψΈΣΒψCΓδΘ§ΒψDΈΣAΓδBΒΡ÷–ΒψΘ§Ν§Ϋ”AD.‘ρΒψAΒΡ‘ΥΕ·¬ΖΨΕ![]() ”κœΏΕΈADΓΔAΓδDΈß≥…ΒΡ“θ”Α≤ΩΖ÷ΟφΜΐ «______.
”κœΏΕΈADΓΔAΓδDΈß≥…ΒΡ“θ”Α≤ΩΖ÷ΟφΜΐ «______.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥―ß–Θ―ß…ζΒΡΗω–‘ΧΊ≥ΛΖΔ’Ι«ιΩωΘ§―ß–ΘΨωΕ®Έß»ΤΓΑ“τά÷ΓΔΧε”ΐΓΔΟά θΓΔ ιΖ®ΓΔΤδΥϋΜνΕ·œνΡΩ÷–Θ§Ρψ≤ΈΦ”ΡΡ“ΜœνΜνΕ·Θ®ΟΩ»Υ÷Μœό“ΜœνΘ©ΒΡΈ ΧβΓ±Θ§‘Ύ»Ϊ–ΘΖΕΈßΡΎΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γΆΦΥυ ΨΒΡΧθ–ΈΆ≥ΦΤΆΦΘ§«κΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ

Θ®1Θ©‘Ύ’β¥ΈΒς≤ι÷–“ΜΙ≤≥ι≤ιΝΥΕύ…ΌΟϊ―ß…ζΘΩ
Θ®2Θ©«σ≤ΈΦ”ΓΑ“τά÷Γ±ΜνΕ·œνΡΩΒΡ»Υ ΐ’Φ≥ι≤ιΉή»Υ ΐΒΡΑΌΖ÷±»Θ°
Θ®3Θ©»τ»Ϊ–Θ”–2400Οϊ―ß…ζΘ§«κΙάΦΤΗΟ–Θ≤ΈΦ”ΓΑΟά θΓ±ΜνΕ·œνΡΩΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
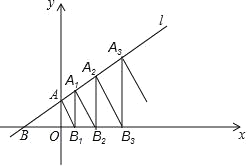
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΘ§A1Θ§A2Θ§A3Γ≠AnΕΦ‘Ύ÷±œΏ1ΘΚyΘΫ![]() x+1…œΘ§ΒψBΘ§B1Θ§B2Θ§B3Γ≠BnΕΦ‘Ύx÷α…œΘ§«“AB1ΓΆ1Θ§B1A1ΓΆx÷αΘ§A1B2ΓΆ1Θ§B2A2ΓΆx÷αΘ§‘ρAnΒΡΚαΉχ±ξΈΣ_________Θ®”ΟΚ§”–nΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΓΘ
x+1…œΘ§ΒψBΘ§B1Θ§B2Θ§B3Γ≠BnΕΦ‘Ύx÷α…œΘ§«“AB1ΓΆ1Θ§B1A1ΓΆx÷αΘ§A1B2ΓΆ1Θ§B2A2ΓΆx÷αΘ§‘ρAnΒΡΚαΉχ±ξΈΣ_________Θ®”ΟΚ§”–nΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΫχ“Μ≤ΫΝΥΫβ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
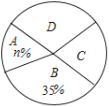
Θ§![]() ΥΡΟϊάœ Π‘Ύ―ß…ζ÷– ήΜΕ”≠ΒΡ≥ΧΕ»Θ§―ß–ΘΥφΜζ≥ι»ΓΝΥ
ΥΡΟϊάœ Π‘Ύ―ß…ζ÷– ήΜΕ”≠ΒΡ≥ΧΕ»Θ§―ß–ΘΥφΜζ≥ι»ΓΝΥ![]() Ηω―ß…ζΫχ––Βς≤ιΘ®±ΜΒς≤ιΒΡ―ß…ζ±Ί–κ―Γ«“÷ΜΡή―ΓΤδ÷–ΒΡ“ΜΟϊάœ ΠΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…ΝΥ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ
Ηω―ß…ζΫχ––Βς≤ιΘ®±ΜΒς≤ιΒΡ―ß…ζ±Ί–κ―Γ«“÷ΜΡή―ΓΤδ÷–ΒΡ“ΜΟϊάœ ΠΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…ΝΥ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ
Θ®1Θ©«σ![]() ΚΆ
ΚΆ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©…»–ΈΆ≥ΦΤΆΦ÷–Θ§![]() Ε‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐ «Εύ…ΌΘΩ
Ε‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐ «Εύ…ΌΘΩ
Θ®3Θ©«σ≥ω![]() ΒΡ»Υ ΐΘ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ°
ΒΡ»Υ ΐΘ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
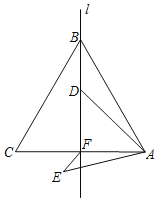
ΓΨΧβΡΩΓΩ»γΆΦΘ§Β»±Ώ»ΐΫ«–ΈΓςABCΒΡ±Ώ≥ΛΈΣ6Θ§l «AC±Ώ…œΒΡΗΏBFΥυ‘ΎΒΡ÷±œΏΘ§ΒψDΈΣ÷±œΏl…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”ADΘ§≤ΔΫΪAD»ΤΒψAΡφ ±’κ–ΐΉΣ60Γψ÷ΝAEΘ§Ν§Ϋ”EFΘ§‘ρEFΒΡΉν–Γ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
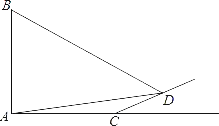
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤλΗΥABΒΡΕΞΕΥB‘ΎœΠ―τΒΡ”ύΜ‘œ¬¬δ‘Ύ“ΜΗω–±Τ¬…œΒΡΒψD¥ΠΘ§Ρ≥–Θ ΐ―ßΩΈΆβ–Υ»Λ–ΓΉιΒΡΆ§―ß’ΐ‘Ύ≤βΝΩΤλΗΥΒΡΗΏΕ»Θ§‘ΎΤλΗΥΒΡΒΉ≤ΩA¥Π≤βΒΟΒψDΒΡ―ωΫ«ΈΣ15ΓψΘ§ACΘΫ10ΟΉΘ§”÷≤βΒΟΓœBDAΘΫ45ΓψΘ°“―÷Σ–±Τ¬CDΒΡΤ¬Ε»ΈΣiΘΫ1ΘΚ![]() Θ§«σΤλΗΥABΒΡΗΏΕ»Θ®
Θ§«σΤλΗΥABΒΡΗΏΕ»Θ®![]() Θ§ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©Θ°
Θ§ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com