
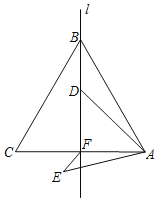
【题目】如图,等边三角形△ABC的边长为6,l是AC边上的高BF所在的直线,点D为直线l上的一动点,连接AD,并将AD绕点A逆时针旋转60°至AE,连接EF,则EF的最小值为_____.
【答案】![]()
【解析】
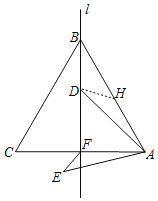
取AB的中点H,连接DH,由“SAS”可证△ADH≌△AEF,可得EF=DH,由垂线段最短,可得当DH⊥BF时,DH的长最短,即EF有最小值,即可求解.
解:如图,取AB的中点H,连接DH,
∵△ABC是等边三角形,BF是高,
∴AF=CF=3,∠ABF=30°,
∵点H是AB中点,
∴BH=AH=3,
∴AH=AF,
∵将AD绕点A逆时针旋转60°至AE,
∴AE=AD,∠DAE=60°=∠BAC,
∴∠DAH=∠FAE,且AF=AH,AD=AE,
∴△ADH≌△AEF(SAS)
∴EF=DH,
∴当DH⊥BF时,DH的长最短,即EF有最小值,
∴DH的最小值为![]() BH=
BH=![]() ,
,
∴EF的最小值为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
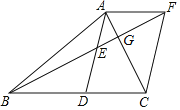
(1)求证:![]() ;
;
(2)若![]() ,①试判断四边形
,①试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
②若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长_________.
的长_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京时间2019年4月10日人类首次直接拍摄到黑洞的照片,它是一个“超巨型”质量黑洞,位于室女座星系团中一个超大质量星系﹣M87的中心,距离地球5500万光年.数据“5500万光年”用科学记数法表示为( )

A.5500×104光年B.055×108光年
C.5.5×103光年D.5.5×107光年
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成相应的任务:
全等四边形
能够完全重合的两个四边形叫做全等四边形.由此可知,全等四边形的对应边相等、对应角相等;反之,四条边分别相等、四个角也分别相等的两个四边形全等.在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件.根据探究三角形全等条件的经验容易发现,满足1个、2个、3个、4个条件时,两个四边形不一定全等.
在探究“满足5个条件的四边形![]() 和四边形
和四边形![]() 是否全等”时,智慧小组的同学提出如下两个命题:
是否全等”时,智慧小组的同学提出如下两个命题:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 四边形
四边形![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 四边形
四边形![]()
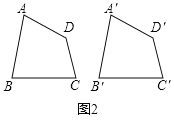
(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是____命题(填“真”或“假”);

(2)小彬经过探究发现命题②是真命题,请你结合图2证明这一命题;
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() ,______,_____,则四边形
,______,_____,则四边形![]() 四边形
四边形![]() ,请在横线上填写两个关于“角”的条件,使该命题为真命题.
,请在横线上填写两个关于“角”的条件,使该命题为真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
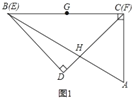
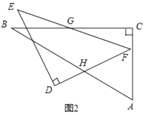
【题目】一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,现将三角板
,现将三角板![]() 绕点
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,点
的变化过程中,点![]() 相应移动的路径长共为____.(结果保留根号)
相应移动的路径长共为____.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
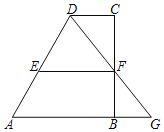
【题目】如图,四边形ABCD中,AB∥CD,CD≠AB,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:CFFG=DFBF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=12,EF=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
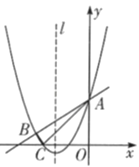
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MC|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com