
【题目】一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
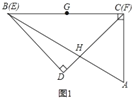
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,现将三角板
,现将三角板![]() 绕点
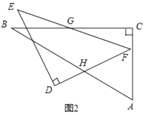
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,点
的变化过程中,点![]() 相应移动的路径长共为____.(结果保留根号)
相应移动的路径长共为____.(结果保留根号)
【答案】![]()
【解析】
当GH⊥DF时,BH的值最小,即点H先从BH=12(![]() - 1)cm,开始向AB方向移动到最小的BH的值,再往BA方向移动到与F重合,求出BH的最大值,则点H运动的总路程为:BH的最大值-BH的最小值+[12(
- 1)cm,开始向AB方向移动到最小的BH的值,再往BA方向移动到与F重合,求出BH的最大值,则点H运动的总路程为:BH的最大值-BH的最小值+[12(![]() -1)-BH的最小值].
-1)-BH的最小值].
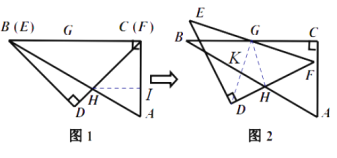
如图2和图3,在∠CGF从0°到60°的变化过程中,点H先向AB方向移,在往BA方向移,直到H与F重合(下面证明此时∠CGF=60度),此时BH的值最大,
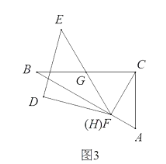
如图3,当F与H重合时,连接CF,因为BG=CG=GF,
所以∠BFC=90度,
∵∠B=30度,
∴∠BFC=60度,
由CG=GF可得∠CGF=60度.
∵BC=12cm,所以BF=![]() BC=6
BC=6![]()
如图2,当GH⊥DF时,GH有最小值,则BH有最小值,且GF//AB,连接DG,交AB于点K,则DG⊥AB,
∵DG=FG,
∴∠DGH=45度,
则KG=KH=![]() GH=
GH=![]() ×(
×(![]() ×6
×6![]() )=3
)=3
BK=![]() KG=3
KG=3![]()
则BH=BK+KH=3![]() +3
+3
则点H运动的总路程为6![]() -(3
-(3![]() +3)+[12(
+3)+[12(![]() -1)-(3
-1)-(3![]() +3)]=12
+3)]=12![]() -18(cm)
-18(cm)
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若![]() ,则
,则![]() =( )
=( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步了解![]() ,
,![]() ,
,![]() ,
,![]() 四名老师在学生中受欢迎的程度,学校随机抽取了
四名老师在学生中受欢迎的程度,学校随机抽取了![]() 个学生进行调查(被调查的学生必须选且只能选其中的一名老师),并将调查结果绘制成了如下两幅不完整的统计图:
个学生进行调查(被调查的学生必须选且只能选其中的一名老师),并将调查结果绘制成了如下两幅不完整的统计图:
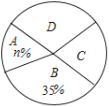
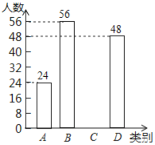
(1)求![]() 和
和![]() 的值;
的值;
(2)扇形统计图中,![]() 对应的圆心角的度数是多少?
对应的圆心角的度数是多少?
(3)求出![]() 的人数,并补全条形统计图.
的人数,并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
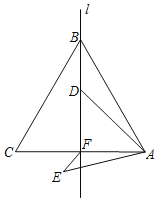
【题目】如图,等边三角形△ABC的边长为6,l是AC边上的高BF所在的直线,点D为直线l上的一动点,连接AD,并将AD绕点A逆时针旋转60°至AE,连接EF,则EF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三位数,它的各个数位上的数字都不为零,且满足百位上的数字与个位上的数字的平均数等于十位上的数字,则称这个三位数为开合数.设![]() 为一个开合数,将
为一个开合数,将![]() 的百位数字与个位数字交换位置后得到的新数再与
的百位数字与个位数字交换位置后得到的新数再与![]() 相加的和记为
相加的和记为![]() .例如:852是“开合数”,则
.例如:852是“开合数”,则![]() .
.
(1)已知开合数![]() (
(![]() ,且为
,且为![]() 整数),求
整数),求![]() 的值;
的值;
(2)三位数![]() 是一个开合数,若百位数字小于个位数字,
是一个开合数,若百位数字小于个位数字,![]() 是一个整数,且
是一个整数,且![]() 能被个位数字与百位数字的差整除,请求满足条件的所有
能被个位数字与百位数字的差整除,请求满足条件的所有![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
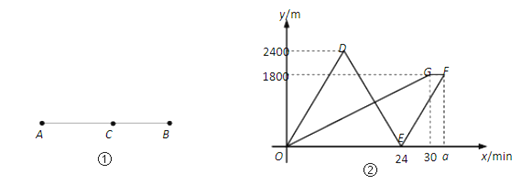
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.
(1)小明的速度为 m/min,图②中a的值为 .
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
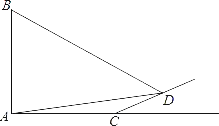
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示,已知每个菱形图案的边长为10![]() cm,其中一个内角为60°.
cm,其中一个内角为60°.
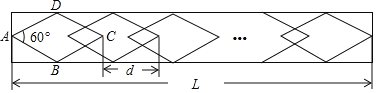
(1)求一个菱形图案水平方向的对角线长;
(2)若d=26,纹饰的长度L能否是6010cm?若能,求出菱形个数;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com