
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
【答案】(1)w=﹣2x2+120x﹣1600;(2)销售单价定为30元时,每天销售利润最大,最大销售利润200元;(3)25元
【解析】试题分析:(1)用每件的利润![]() 乘以销售量即可得到每天的销售利润,即
乘以销售量即可得到每天的销售利润,即![]() 然后化为一般式即可;
然后化为一般式即可;
(2)把(1)中的解析式进行配方得到顶点式![]() 然后根据二次函数的最值问题求解;
然后根据二次函数的最值问题求解;
(3)求函数值为150所对应的自变量的值,即解方程![]() 然后利用销售价不高于每件28元确定
然后利用销售价不高于每件28元确定![]() 的值.
的值.
试题解析:(1)根据题意可得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 与
与![]() 之间的函数关系为:
之间的函数关系为:![]() ;
;
(2)根据题意可得:![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() 最大值为200.
最大值为200.
答:销售单价定为30元时,每天销售利润最大,最大销售利润200元.
(3)当![]() 时,可得方程
时,可得方程![]() .
.
解得![]() ,
,
∵![]() ,∴
,∴![]() 不符合题意,应舍去.
不符合题意,应舍去.
答:该商店销售这种健身球每天想要获得150元的销售利润,销售单价定为25元.


科目:初中数学 来源: 题型:
【题目】计算
(1)![]()
(2)(+6)-(+12)+(+9.6)-(+7.6)
(3)5×![]() ―
―![]() ×
×![]()
(4)(![]() )×(-60 )
)×(-60 )
(5)(2![]() )-(+10
)-(+10![]() )+(-8
)+(-8![]() )-(+3)
)-(+3)
(6)﹣14﹣(1﹣0.5)×![]() ×[1﹣(﹣2)2];
×[1﹣(﹣2)2];
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】进价为每件40元的某商品,售价为每件50元时,每星期可卖出500件,市场调查反映:如果每件的售价每降价1元,每星期可多卖出100件,但售价不能低于每件42元,且每星期至少要销售800件.设每件降价x元 (x为正整数),每星期的利润为y元.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
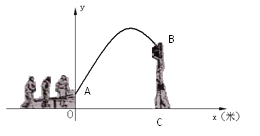
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E、F分别为BC、CD边上的两个动点,∠EAF=45°,下列几个结论中:①EF=BE+DF;②MN2=BM2+DN2;③FA平分∠DFE;④连接MF,则△AMF为等腰直角三角形;⑤∠AMN=∠AFE. 其中一定成立的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长方形ABCD中,AB=CD=8cm,AD=BC=6cm,点E是DC边上一点,且CE=1cm,动点P从A点出发,沿折线A-D-E以acm/s的速度向终点E运动,运动时间为t秒,已知a是方程![]() 的解.
的解.
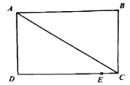
(1)求a的值;
(2)点P在运动过程中,请用t的式子表示△APC的面积;
(3)在点P运动的同时,有一动点Q从C点出发,沿折线C-D-A以1cm/s的速度向终点A运动,运动过程中,一个点停止运动时另一个点继续向终点运动,当△APC和△AQC的面积相差6平方厘米时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
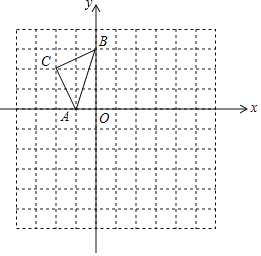
【题目】如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
(1)将△ABC绕原点O顺时针旋转90°得到△A1B1C1,画出△A1B1C1;
(2)以点O为位似中心,与△ABC位似的△A2B2C2满足A2B2:AB=2:1,请在网格内画出△A2B2C2,并直接填写△A2B2C2的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
1637 年笛卡儿(R.Descartes,1596 1650)在其《几何学》中,首次应用待定系数法将 4 次方程分解为两个 2 次方程求解,并最早给出因式分解定理.
他认为,若一个高于二次的关于 x 的多项式能被 (![]() ) 整除,则其一定可以分解为 (
) 整除,则其一定可以分解为 (![]() ) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
例如:多项式![]() 可以分解为 (
可以分解为 (![]() ) 与另外一个整式 M 的乘积,即
) 与另外一个整式 M 的乘积,即 ![]()
令![]() 时,可知 x =1 为该方程的一个根.
时,可知 x =1 为该方程的一个根.
关于笛卡尔的“待定系数法”原理,举例说明如下: 分解因式:![]()
观察知,显然 x=1 时,原式 = 0 ,因此原式可分解为 (![]() ) 与另一个整式的积.
) 与另一个整式的积.
令:![]() ,则
,则![]() =
=![]() ,因等式两边 x 同次幂的系数相等,则有:
,因等式两边 x 同次幂的系数相等,则有: ,得
,得![]() ,从而
,从而![]()
此时,不难发现 x= 1 是方程 ![]() 的一个根.
的一个根.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求 a 的值并将多项式
的因式,求 a 的值并将多项式![]() 分解因式;
分解因式;
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求a+ b 的值.
,求a+ b 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com