
【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

【答案】(1)BE是⊙O的切线;(2)![]() .
.
【解析】试题分析:(1)结论:BE是⊙O的切线.首先证明∠OAP=90°,再证明△EOB≌△EOA,推出∠OBE=∠OAE即可解决问题.
(2)由(1)可知AB=2BF,在Rt△BEO中,∠OBE=90°,OB=4,BE=3,可得OE=![]() =5,由
=5,由![]() BEOB=
BEOB=![]() OEBF,可得BF=
OEBF,可得BF=![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:(1)BE是⊙O的切线.
理由:如图连接OA.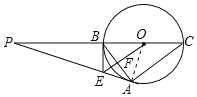
∵PA是切线,
∴PA⊥OA,
∴∠OAP=90°,
∵BC是直径,
∴∠BAC=90°,
∵OE∥AC,
∴∠OFB=∠BAC=90°,
∴OE⊥AB,
∴BF=FA,
∵OB=OA,
∴∠EOB=∠EOA,
在△EOB和△EOA中,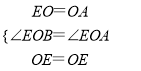 ,
,
∴△EOB≌△EOA,
∴∠OBE=∠OAE=90°,
∴OB⊥BE,
∴BE是⊙O的切线.
(2)由(1)可知AB=2BF,
在Rt△BEO中,∵∠OBE=90°,OB=8,BE=6,
∴OE=![]() =5,
=5,
∵![]() BEOB=
BEOB=![]() OEBF,
OEBF,
∴BF=![]() =
=![]() ,
,
∴AB=2BF=![]()
.


科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b、c在数轴上的位置如图所示.
![]()
(1)化简:|a|= |b|= ;
(2)比较大小a﹣c 0,a+b 0.
(3)将a,b,c,﹣a,﹣b,﹣c按从小到大的顺序,用“<”号连接.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点,∠F=90°,∠E=30°.
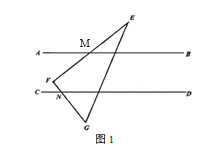
(1)求证:∠EMB+∠DNG=90°
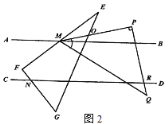
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年4月23日,是第25个世界读书日.为了解学生每周阅读时间,某校随机抽取了部分学生进行调查,根据调查结果,将阅读时间x(单位:小时)分成了4组,A:0≤x<2;B:2≤x<4;C:4≤x<6;D:6≤x<8,试结合图中所给信息解答下列问题:
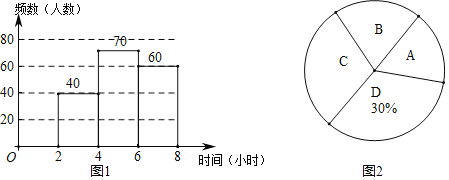
(1)这次随机抽取了 名学生进行调查;扇形统计图中,扇形B的圆心角的度数为 .
(2)补全频数分布直方图;
(3)若该校共有2000名学生,试估计每周阅读时间不少于4小时的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每天超出计划的量数 |
|
|
|
|
|
|
|
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
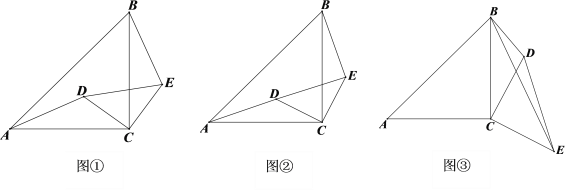
【题目】如图①已知△ACB和△DCE为等腰直角三角形,按如图的位置摆放,直角顶点
C重合.
(1)求证:AD=BE;
(2)将△DCE绕点C旋转得到图②,点A、D、E在同一直线上时,若CD=![]() ,BE=3,
,BE=3,
求AB 的长;
(3)将△DCE绕点C顺时针旋转得到图③,若∠CBD=45°,AC=6,BD=3,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com