
【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点,∠F=90°,∠E=30°.
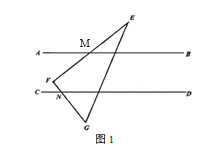
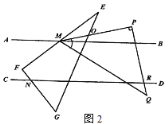
(1)求证:∠EMB+∠DNG=90°
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
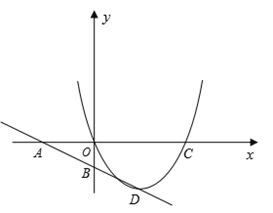
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx的图象过点 (2,0),(-1,6).
(1)求二次函数的关系式;
(2)写出它的对称轴和顶点坐标;
(3)请说明x在什么范围内取值时,函数值y<0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°,∠DBF=14°,∠ADC的度数为_______°.
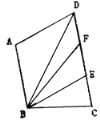
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:
![]()
(1)从中2张卡片,使这2张卡片上数字的乘积最大,如何抽取,最大值是多少?
(2)从中抽取2张卡片,使这两张卡片数相除的商最小,如何抽取,最小值是多少?
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子.(要写出两种运算式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为
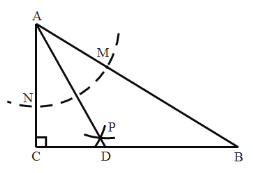
①![]() 是
是![]() 的平分线;
的平分线;
②若![]() ,则
,则![]() ;
;
③![]() ;
;
④点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() 的图象上,点D的坐标为
的图象上,点D的坐标为![]() .将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
.将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com