
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
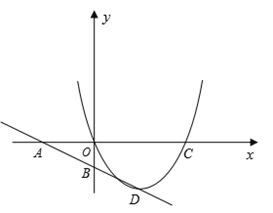
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
【答案】(1)![]() ;(2)点
;(2)点![]() ;(3)
;(3)![]() .
.
【解析】试题分析: ![]() 先求出点
先求出点![]() 的坐标,把点
的坐标,把点![]() 的坐标代入抛物线即可求出抛物线的解析式.
的坐标代入抛物线即可求出抛物线的解析式.
![]() 分两种情况进行讨论.
分两种情况进行讨论.
![]() 在
在![]() 中,用余弦得到
中,用余弦得到![]() 设
设![]() 根据勾股定理求出
根据勾股定理求出![]() 的值,求出点
的值,求出点![]() 的坐标,根据待定系数法求出直线的解析式.
的坐标,根据待定系数法求出直线的解析式.
试题解析:
(1)由题知:D点的横坐标为2,
∴![]() ,
,
![]() 把
把![]() 代入抛物线:
代入抛物线: ![]() 解之得:
解之得: 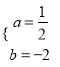
∴抛物线的解析式为: ![]()
(2)存在点![]()
设对称轴与![]() 轴交于点
轴交于点![]() ,
, ![]()
易知: ![]()
![]()
情况1: ![]() 点在
点在![]() 点上方,则
点上方,则![]()
若![]() 则
则![]()
∴![]() 解得:
解得: ![]() ,
,
∴![]() .
.
若![]() 则
则![]()
![]() 解得:
解得: ![]()
∴ ![]() .
.
情况2:若P在D点的下方,则![]() 没有一个角会为
没有一个角会为![]()
∴![]() 与
与![]() 不可能相似
不可能相似
综上可知:存在点![]()
(3)、设![]() 与
与![]() 轴交于点
轴交于点![]() ,连NC交抛物线对称轴于一点,即为圆心M点,
,连NC交抛物线对称轴于一点,即为圆心M点,

![]()
在![]() 中,
中, ![]()
![]() 设
设![]()
则: ![]() 解得:
解得: ![]()
![]() ∴点
∴点![]() 坐标为(0,8),
坐标为(0,8),
![]()
设过点![]() 且与
且与![]() 相切的直线为
相切的直线为![]()
则![]() ,把
,把![]() 点代入有:
点代入有: ![]() ,解得:
,解得: ![]()
∴过点![]() 且与
且与![]() 相切的直线为
相切的直线为 ![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数轴上5与﹣2所对的两点之间的距离:|5﹣(﹣2)|=7;
在数轴上﹣2与3所对的两点之间的距离:|﹣2﹣3|=5;
在数轴上﹣8与﹣5所对的两点之间的距离:|(﹣8)﹣(﹣5)|=3
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离AB=|a﹣b|=|b﹣a|
回答下列问题:
(1)数轴上表示﹣2和﹣5的两点之间的距离是_____;
数轴上表示数x和3的两点之间的距离表示为_____;
数轴上表示数_____和_____的两点之间的距离表示为|x+2|,;
(2)七年级研究性学习小组在数学老师指导下,对式子|x+2|+|x﹣3|进行探究:
①请你在草稿纸上画出数轴,当表示数x的点在﹣2与3之间移动时,|x﹣3|+|x+2|的值总是一个固定的值为:_____.
②请你在草稿纸上画出数轴,要使|x﹣3|+|x+2|=7,数轴上表示点的数x=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的2倍.
,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]() .
.
化简,得: ![]() .
.
这种利用方程根的代替求新方程的方法,我们成为“换根法”,请用阅读材料提供的“换根法”求新方程![]() 要求:把所求方程化成一般形式
要求:把所求方程化成一般形式![]() ;
;
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数.
,求一个一元二次方程,使它的根分别是已知方程根的相反数.
(2)已知关于x的一元二次方程![]() 有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() ,且
,且![]() 和
和![]() 之间的距离为
之间的距离为![]() ,小明同学制作了一个直角三角形硬纸板
,小明同学制作了一个直角三角形硬纸板![]() ,其中
,其中![]() ,
,![]() ,
,![]() .小明利用这块三角板进行了如下的操作探究:
.小明利用这块三角板进行了如下的操作探究:
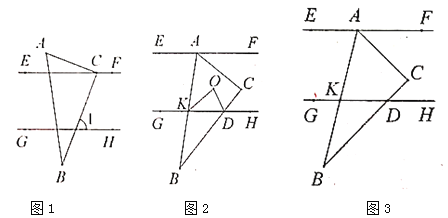
(1)如图1,若点![]() 在直线
在直线![]() 上,且
上,且![]() .求
.求![]() 的度数;
的度数;
(2)若点![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 和
和![]() 之间(不含
之间(不含![]() 、
、![]() 上),边
上),边![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 和点
和点![]() .
.
①如图2,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .在
.在![]() 绕着点
绕着点![]() 旋转的过程中,
旋转的过程中,![]() 的度数是否变化?若不变,求出
的度数是否变化?若不变,求出![]() 的度数;若变化,请说明理由;
的度数;若变化,请说明理由;
②如图3,在![]() 绕着点
绕着点![]() 旋转的过程中,设
旋转的过程中,设![]() ,
,![]() ,求
,求![]() 的取值范
的取值范
查看答案和解析>>
科目:初中数学 来源: 题型:
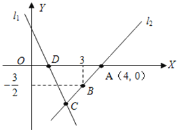
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() 经过点A,点B,直线
经过点A,点B,直线![]() ,
,![]() 交于点C.
交于点C.
(1)求直线![]() 的解析表达式;
的解析表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得
上存在异于点C的另一点P,使得![]() 的面积等于
的面积等于![]() 面积,请直接写出点P的坐标.
面积,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点,∠F=90°,∠E=30°.
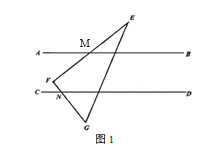
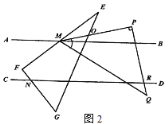
(1)求证:∠EMB+∠DNG=90°
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com