
����Ŀ�����⣺��֪����![]() ����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
�⣺�����̵ĸ�Ϊy����![]() ������
������![]() ��
��
��![]() ������֪���̣���
������֪���̣���![]() ��
��
���ã� ![]() ��
��
�������÷��̸��Ĵ������·��̵ķ��������dz�Ϊ�����������������Ķ������ṩ�ġ������������·���![]() Ҫ�����̻���һ����ʽ
Ҫ�����̻���һ����ʽ![]() ��
��
(1)��֪����![]() ����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸����෴����
����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸����෴����
(2)��֪����x��һԪ���η���![]() ���������������ʵ��������һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸��ĵ�����
���������������ʵ��������һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸��ĵ�����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϣ���A��ʾ��10����B��ʾ11����C��ʾ18������P�ӵ�A��������������������ÿ��2����λ���ٶ������˶���ͬʱ������Q�ӵ�C�����������Ḻ������ÿ��1����λ���ٶ������˶������˶�ʱ��Ϊt�룮
��1����tΪ��ֵʱ��P��Q����������������M����Ӧ�����Ƕ��٣�
��2���ڵ�Q�������B֮ǰ����tΪ��ֵʱ����P����O�ľ������Q����B�ľ�����ȣ�
��3���ڵ�P�����˶��Ĺ����У�N��AP���е㣬�ڵ�P�����C֮ǰ����2CN��PC��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
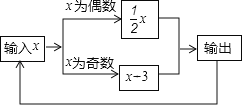
����Ŀ����ͼ������һ����ֵת�����������������һ���������Ϊ7�����2018�����������_____������һ���������Ϊx��ʹ��2���������Ҳ��x����x��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������������A��B��C���ش��������⣺
(1)������B�����ƶ�6����λ������������ʾ��������С�����Ƕ��٣�
(2)����������һ��D��ʹ��D��A��C����ľ�����ȣ�д����D��ʾ������
(3)�ڵ�B�����һ��E��ʹ��E����A�ľ����ǵ���B�ľ����2������д����E��ʾ������
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019Ů�����籭��9��14����29�����ձ����У�����Ϊ��ѭ����������ÿ������֮�����һ������һ������66�����й�Ů����ȫʤ�ɼ��������籭�ھ���Ϊ����70�������ϴ������й����ڱ������籭��������ʤ�� ��
A.10��B.11��C.12��D.13��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�и��������������⣺
![]()
��1���������ͼ��A��B�����λ�ã��ֱ�д����������ʾ��������Ϊ��������������
��2���۲����ᣬ���A�ľ���Ϊ4�ĵ��ʾ��������������������
��3������������۵���ʹ�õ�A���ʾ��2�ĵ��غϣ����B���ʾ���������������ĵ��غϣ�
��4�����������M��N����֮��ľ���Ϊ2020��M��N����ࣩ����M��N���㾭����3�����۵������غϣ���M��N��������ʾ�����ֱ�����������������������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�A����
�ύ�ڵ�A����![]() �ύ�ڵ�B��������
�ύ�ڵ�B��������![]() ����ԭ��͵�C��4,0��������D��ֱ��AB�ϡ�
����ԭ��͵�C��4,0��������D��ֱ��AB�ϡ�
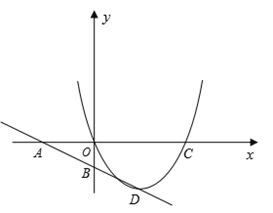
��1������������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ����P��C��DΪ��������������ACD���ơ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3����Q��![]() ���Ϸ����������ϵ�һ�����㣬��
���Ϸ����������ϵ�һ�����㣬��![]() ����M������O��C��Q�����C�������M���е�ֱ�߽���ʽ
����M������O��C��Q�����C�������M���е�ֱ�߽���ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У����������������A��B��C���������¶��壺�����ε��κ�һ���߾���ij��������ƽ�У���A��B��C���㶼�ھ��ε��ڲ���߽��ϣ���Ƹþ���Ϊ��A��B��C�ġ�������Ρ����ڵ�A��B��C�����С�������Ρ��У������������С�ľ��Σ���Ƹþ���Ϊ��A��B��C�ġ�����������Ρ���
��ͼ1������DEFG������IJCH���ǵ�A��B��C�ġ�������Ρ�������IJCH�ǵ�A��B��C�ġ�����������Ρ���
��ͼ2����֪M(4��1)��N(-2��3)����P(m��n)��
��1������m��1��n��4�����M��N��P�ġ�����������Ρ����ܳ�Ϊ �����Ϊ ��
����m��1����M��N��P�ġ�����������Ρ������Ϊ24����n��ֵ��
��2������P��ֱ��y��-2x��4�ϣ�����M��N��P�ġ�����������Ρ�Ϊ������ʱ��ֱ��д����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
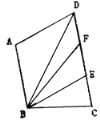
����Ŀ����ͼ,AB��CD,��EΪCD��һ��,����BE,AD��BE,����BD,BDƽ�֡�ABE,BFƽ�֡�ABC��CD�ڵ�F, ��ABC=100������DBF=14��,��ADC�Ķ���Ϊ_______��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com