
【题目】根据图中给出的数轴解答问题:
![]()
(1)请你根据图中A,B两点的位置,分别写出他们所表示的有理数为 ;
(2)观察数轴,与点A的距离为4的点表示的数是 ;
(3)如果将数轴折叠,使得点A与表示﹣2的点重合,则点B与表示数 的点重合;
(4)如果数轴上M,N两点之间的距离为2020(M在N的左侧),且M,N两点经过(3)中折叠后互相重合,则M,N两点所表示的数分别是 , .![]()
【答案】(1)1,﹣2.5;(2)﹣3或5;(3)1.5;(4)﹣1010.5,1009.5.
【解析】
(1)(2)观察数轴,直接得出结论;
(3)A点与-2表示的点相距3个单位,其对称点为-0.5,由此得出与B点重合的点;
(4)对称点为-0.5,M点在对称点左边,距离对称点2020÷2=1010个单位,N点在对称点右边,离对称点1010个单位,由此求出M、N两点表示的数.
(1)由数轴可知,A点表示数1,B点表示数﹣2.5.
(2)A点表示数1,与点A的距离为4的点表示的数是:﹣3或5.
(3)当A点与﹣2表示的点重合,则B点与数1.5表示的点重合.
(4)由对称点为﹣0.5,且M、N两点之间的距离为2020(M在N的左侧)可知,
点M、N到﹣1的距离为2020÷2=1010,
所以,M点表示数﹣0.5﹣1010=﹣1010.5,N点表示数﹣0.5+1010=1009.5.


科目:初中数学 来源: 题型:
【题目】如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
(1)当点D运动到AB的中点时,直接写出AE的长.
(2)当DF⊥AB时,求AD的长.
(3)在运动过程中线段GE的长是否发生变化?如果不变,求出线段GE的长:如果发生改变请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,定义直线![]() 与双曲线
与双曲线![]() 的交点
的交点![]() 、n为正整数
、n为正整数![]() 为“双曲格点”,双曲线
为“双曲格点”,双曲线![]() 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
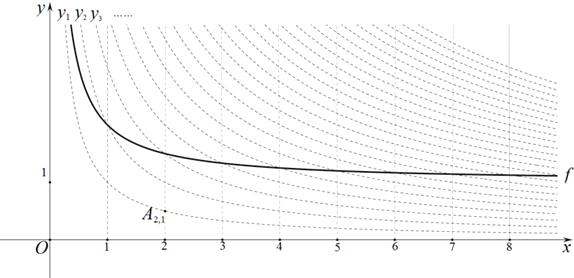
![]() “双曲格点”
“双曲格点”![]() 的坐标为______;
的坐标为______; ![]() 若线段
若线段![]() 的长为1个单位长度,则
的长为1个单位长度,则![]() ______;
______;
![]() 图中的曲线f是双曲线
图中的曲线f是双曲线![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点![]() ,则f的解析式为
,则f的解析式为![]() ______;
______;
![]() 画出双曲线
画出双曲线![]() 的“派生曲线”
的“派生曲线”![]() 与双曲线
与双曲线![]() 不重合
不重合![]() ,使其经过“双曲格点”
,使其经过“双曲格点”![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的2倍.
,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]() .
.
化简,得: ![]() .
.
这种利用方程根的代替求新方程的方法,我们成为“换根法”,请用阅读材料提供的“换根法”求新方程![]() 要求:把所求方程化成一般形式
要求:把所求方程化成一般形式![]() ;
;
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数.
,求一个一元二次方程,使它的根分别是已知方程根的相反数.
(2)已知关于x的一元二次方程![]() 有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰兴市为进一步改善生态环境决定对街道进行绿化建设,为此准备购进甲、乙两种树木、已知甲种树木的单价为![]() 元,乙种树木的单价为
元,乙种树木的单价为![]() 元.
元.
(1)若![]() 街道购买甲、乙两种树木共花费
街道购买甲、乙两种树木共花费![]() 元,其中,乙种树木是甲种树木的一半多
元,其中,乙种树木是甲种树木的一半多![]() 棵,请求出该街道购买的甲、乙两种树木各多少棵;
棵,请求出该街道购买的甲、乙两种树木各多少棵;
(2)相关资料表明:甲种树木的成活率为![]() ,乙种树木的成活率为
,乙种树木的成活率为![]() .现
.现![]() 街道购买甲、乙两种树木共
街道购买甲、乙两种树木共![]() 棵,为了使这批树木的总成活率不低于
棵,为了使这批树木的总成活率不低于![]() ,则甲种树木至多购买多少棵?
,则甲种树木至多购买多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() ,且
,且![]() 和
和![]() 之间的距离为
之间的距离为![]() ,小明同学制作了一个直角三角形硬纸板
,小明同学制作了一个直角三角形硬纸板![]() ,其中
,其中![]() ,
,![]() ,
,![]() .小明利用这块三角板进行了如下的操作探究:
.小明利用这块三角板进行了如下的操作探究:
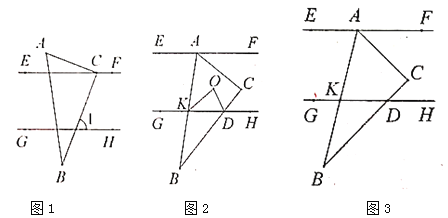
(1)如图1,若点![]() 在直线
在直线![]() 上,且
上,且![]() .求
.求![]() 的度数;
的度数;
(2)若点![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 和
和![]() 之间(不含
之间(不含![]() 、
、![]() 上),边
上),边![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 和点
和点![]() .
.
①如图2,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .在
.在![]() 绕着点
绕着点![]() 旋转的过程中,
旋转的过程中,![]() 的度数是否变化?若不变,求出
的度数是否变化?若不变,求出![]() 的度数;若变化,请说明理由;
的度数;若变化,请说明理由;
②如图3,在![]() 绕着点
绕着点![]() 旋转的过程中,设
旋转的过程中,设![]() ,
,![]() ,求
,求![]() 的取值范
的取值范
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,一条生产线的流水线上依次有5个机器人,它们站立的位置在数轴上依次用点A1,A2,A3,A4,A5表示.

(1)若原点是零件的供应点,5个机器人分别到供应点取货的总路程是多少?
(2)若将零件的供应点改在A1,A3,A5中的其中一处,并使得5个机器人分别到达供应点取货的总路程最短,你认为应该在哪个点上?通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120).已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
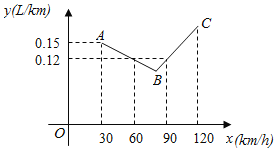
(1)当30≤x≤120时,求y与x之间的函数表达式;
(2)该汽车的速度是多少时,耗油量最低?最低是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com