
����Ŀ��̩����Ϊ��һ��������̬���������Խֵ������̻����裬Ϊ���������ס���������ľ����֪������ľ�ĵ���Ϊ![]() Ԫ��������ľ�ĵ���Ϊ
Ԫ��������ľ�ĵ���Ϊ![]() Ԫ.
Ԫ.
(1)��![]() �ֵ�����ס���������ľ������
�ֵ�����ס���������ľ������![]() Ԫ�����У�������ľ�Ǽ�����ľ��һ���
Ԫ�����У�������ľ�Ǽ�����ľ��һ���![]() �ã�������ýֵ�����ļס���������ľ�����ٿã�
�ã�������ýֵ�����ļס���������ľ�����ٿã�
(2)������ϱ�����������ľ�ijɻ���Ϊ![]() ��������ľ�ijɻ���Ϊ
��������ľ�ijɻ���Ϊ![]() .��
.��![]() �ֵ�����ס���������ľ��
�ֵ�����ס���������ľ��![]() �ã�Ϊ��ʹ������ľ���ܳɻ��ʲ�����
�ã�Ϊ��ʹ������ľ���ܳɻ��ʲ�����![]() ���������ľ�������ٿã�
���������ľ�������ٿã�
���𰸡���1��������ľ��![]() �ã�������ľ
�ã�������ľ![]() �ã���2��������ľ�����
�ã���2��������ľ�����![]() .
.
��������
��1���������ľx�ã�������y�ã��ؼ�������ס���������ľ������34000Ԫ�����У�������ľ�Ǽ�����ľ��һ���120�ã����ݵ�����ϵ�г����̲����
��2����������繺��a�ã����������繺��500-a���ã���������ɵò��ȹ�ϵ����������ijɻ���+��������ijɻ�����92%��500����ɵô𰸣�
��1���������ľ��![]() �ã�������ľ��
�ã�������ľ��![]() �ã��������⣬��
�ã��������⣬��
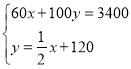
��ã�![]()
�𣺼�����ľ��![]() �ã�������ľ
�ã�������ľ![]() ��.
��.
��2����������繺��a�ã����������繺��800-a���ã�������ã�
90%a+95%��500-a����92%��500��
��ã�a��300��
��a������
��a=300��
�𣺼������������300�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������a��b�������ϵĶ�Ӧ����ͼ��ʾ��
��1����֪a=�C2.3��b=0.4������|a+b|�C|a|�C|1�Cb|��ֵ��
��2����֪������a��b������|a+b|�C|a|�C|1�Cb|��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���εο쳵��һ�ֱ�ݵij��й��ߣ���Ƽ۹�����ͼ��

��ע���εο쳵��������̷ѡ�ʱ���ѡ�Զ;�������ֹ��ɣ�������̷Ѱ��г��ľ���ʱ�α���ʵ����̼��㣺ʱ���Ѱ�����ʱ�α����г���ʵ��ʱ����㣬Զ;�ѵ���ȡ��ʽ���г����10�������ڣ���10�������Զ;�ѣ�����10����ģ���������ÿ������0.3Ԫ��
��1��С������7��00�Ӽҳ��������εο쳵��ѧУ����ʻ���2�����ʱ8���ӣ��踶������ ��Ԫ������17��00��ѧ�����εο쳵�����赥λ����ʻ���5�����ʱ20���ӣ��踶������ ��Ԫ��
��2��ij��06��10�����������εο쳵��ij�أ���ʻ���20�����ʱ40���ӣ��踶���Ѷ���Ԫ��
��3��ij����ͨʱ�γ����ݵο쳵��ij�أ���ʱ30���ӣ���������39.8Ԫ��������ʻ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1�������ɸ�СԲȦ�ѳɵ�һ������ȱ������ε�ͼ����������һ����һ��ԲȦ��
���¸��������һ���һ��ԲȦ��һ������n �㣮��ͼ1���ú���ԭͼ1ƴ��ͼ2����״���������ǿ���
���ͼ1������ԲȦ�ĸ���Ϊ1��2��3������n��![]() ��
��
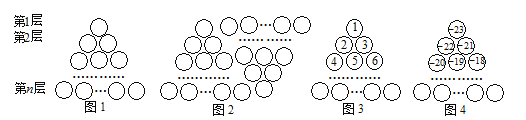
���ͼ�е�ԲȦ����13�㣬�����������⣺
��1�������������£���ÿ��ԲȦ�а�ͼ3�ķ�ʽ����һ��������������1��2��3��4������������ײ�����
�����ԲȦ�е����� ��
��2�������������£���ÿ��ԲȦ�а�ͼ4�ķ�ʽ����һ��������������23����22����21����20����������
��ײ����ұ�ԲȦ�ڵ�����_______��
��3����ͼ4������ԲȦ�и����ľ���ֵ֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�и��������������⣺
![]()
��1���������ͼ��A��B�����λ�ã��ֱ�д����������ʾ��������Ϊ��������������
��2���۲����ᣬ���A�ľ���Ϊ4�ĵ��ʾ��������������������
��3������������۵���ʹ�õ�A���ʾ��2�ĵ��غϣ����B���ʾ���������������ĵ��غϣ�
��4�����������M��N����֮��ľ���Ϊ2020��M��N����ࣩ����M��N���㾭����3�����۵������غϣ���M��N��������ʾ�����ֱ�����������������������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0��������������y=![]() x��ͼ����ͼ��ʾ����ax2+��b��
x��ͼ����ͼ��ʾ����ax2+��b��![]() ��x+c=0��a��0��������֮���� ��
��x+c=0��a��0��������֮���� ��

A. ����0 B. ����0 C. С��0 D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ��Ѳ����Ħ�г���һ���ϱ������Ѳ�ߣ����Ӹ�ͤ�������涨��ͤΪԭ�㣬��Ϊ�������ʱ����ʻ��¼���£���λ��ǧ�ף� +10��-9��+7��-15��+6��-14��+4��-2
��1�����ͣ���ĵط��ڸ�ͤ���ĸ��������ͤ��Զ��
��2����Ħ�г���ʻ��ÿǧ����0.06����ÿ��6.2Ԫ������ظ�ͤ����һ����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѿ���ij�ֹ��ɵ�һ������1,��2,3,��4,5,��6��...�����г���������Σ�
 ........
........
̽�������¼���
��1����10�еĵ�1������ʲô����
��2������2019ǰ���Ǹ��Ż�������?�ڵڼ���?�ڼ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�E��CB�ӳ�����һ�����㣬F��G�ֱ�ΪAE��BC���е㣬FG��ED�ཻ�ڵ�H��
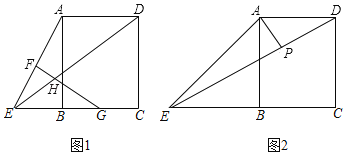
��1����֤��HE��HG��
��2����ͼ2����BE��ABʱ������A��AP��DE�ڵ�P������BP����PQ��PB��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com