
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
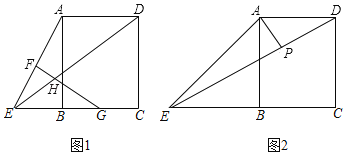
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求PQ与PB的数量关系,并说明理由.
【答案】(1)见解析;(2)PQ![]() PB,理由见解析.
PB,理由见解析.
【解析】
(1)连接AG,并延长AG交DC的延长线于M,连接EM,G为BC的中点,根据矩形的性质得出∠ABG=∠DCB=90°,根据全等三角形的判定得出△ABG≌△MCG,根据全等三角形的性质得出GA=GM,求出FG∥EM,根据平行线的性质得出∠HGE=∠MEC,求出△DEC≌△MEC,根据全等三角形的性质得出∠DEC=∠MEC,求出∠HEG=∠HGE即可;
(2)过点B作BQ⊥BP交DE于Q,求出∠APE=∠ABE=90°,∠BEQ=∠BAP,∠EBQ=∠ABP,根据全等三角形的判定得出△BEQ≌△BAP,根据全等三角形的性质得出BQ=BP,PA=QE,求出△PBQ是等腰直角三角形,即可得出答案.
(1)证明:连接AG,并延长AG交DC的延长线于M,连接EM,
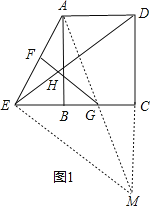
∵G为BC的中点,
∴BG=CG,
∵四边形ABCD是矩形,
∴∠ABG=∠DCB=90°,
∴∠ABG=∠MCG=90°,
在△ABG和△MCG中,
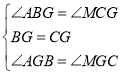 ,
,
∴△ABG≌△MCG(ASA),
∴GA=GM,
∵F为AE的中点,
∴FA=FE,
∴FG是△AEM的中位线,
∴FG∥EM,
∴∠HGE=∠MEC,
在△DCE和△MCE中,
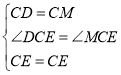 ,
,
∴△DEC≌△MEC(SAS),
∴∠DEC=∠MEC,
∵∠HGE=∠MEC,
∴∠HEG=∠HGE,
∴HE=HG;
(2)答:PQ![]() PB
PB
理由:过点B作BQ⊥BP交DE于Q,则∠QBP=90°,
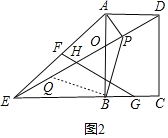
∵AP⊥DE,四边形ABCD是矩形,
∴∠APE=∠ABE=90°,
∵∠APO+∠AOP+∠BAP=180°,∠EOB+∠ABE+∠BEP=180°,∠AOP=∠EOB,
∴∠BEQ=∠BAP,
∵∠QBP=∠ABE=90°,
∴∠EBQ=∠ABP=90°﹣∠ABQ,
在△ABP和△EBQ中,
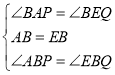 ,
,
∴△BEQ≌△BAP(ASA),
∴BQ=BP,PA=QE,
∴△PBQ是等腰直角三角形,
∴PQ![]() PB.
PB.


科目:初中数学 来源: 题型:
【题目】泰兴市为进一步改善生态环境决定对街道进行绿化建设,为此准备购进甲、乙两种树木、已知甲种树木的单价为![]() 元,乙种树木的单价为
元,乙种树木的单价为![]() 元.
元.
(1)若![]() 街道购买甲、乙两种树木共花费
街道购买甲、乙两种树木共花费![]() 元,其中,乙种树木是甲种树木的一半多
元,其中,乙种树木是甲种树木的一半多![]() 棵,请求出该街道购买的甲、乙两种树木各多少棵;
棵,请求出该街道购买的甲、乙两种树木各多少棵;
(2)相关资料表明:甲种树木的成活率为![]() ,乙种树木的成活率为
,乙种树木的成活率为![]() .现
.现![]() 街道购买甲、乙两种树木共
街道购买甲、乙两种树木共![]() 棵,为了使这批树木的总成活率不低于
棵,为了使这批树木的总成活率不低于![]() ,则甲种树木至多购买多少棵?
,则甲种树木至多购买多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连接DE,CF.
BC,连接DE,CF.
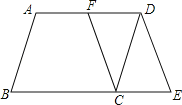
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=10,∠B=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线y![]() x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120).已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
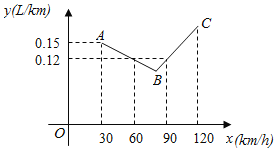
(1)当30≤x≤120时,求y与x之间的函数表达式;
(2)该汽车的速度是多少时,耗油量最低?最低是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=6,P为AD上一动点,把△ABP沿BP翻折,使点A落在点F处,连接CF,若BF=CF,则AP的长为_____.
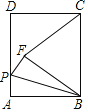
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,图形
中,图形![]() 的投影矩形定义如下:矩形的两组对边分别平行于
的投影矩形定义如下:矩形的两组对边分别平行于![]() 轴,
轴,![]() 轴,图形
轴,图形![]() 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为
的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为![]() ,我们称常数
,我们称常数![]() 为图形
为图形![]() 的投影比,如图1,矩形
的投影比,如图1,矩形![]() 为
为![]() 的投影矩形,其投影比
的投影矩形,其投影比![]() .
.
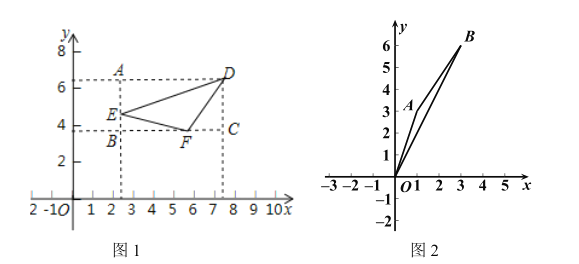
(1)如图2,若点![]() ,则
,则![]() 投影比
投影比![]() 的值为________________;
的值为________________;
(2)已知点![]() ,点
,点![]() ,且
,且![]() 投影比
投影比![]() ,则
,则![]() 点坐标可能是__________(填写序号);
点坐标可能是__________(填写序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(3)已知点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() 和一动点
和一动点![]() ,且
,且![]() ,是否存在这样的
,是否存在这样的![]() ,使得
,使得![]() 的投影比
的投影比![]() 为定值?若存在,请求出
为定值?若存在,请求出![]() 的范围及定值
的范围及定值![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
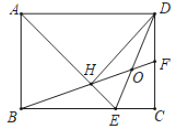
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com