
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为
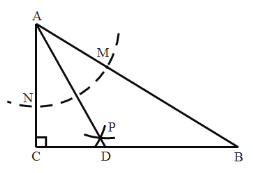
①![]() 是
是![]() 的平分线;
的平分线;
②若![]() ,则
,则![]() ;
;
③![]() ;
;
④点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
A.1个B.2个C.3个D.4个
【答案】C
【解析】
连接PM,PN,证明APNAPM,即可判断①;由![]() ,
,![]() ,得:∠BAC=60°,结合
,得:∠BAC=60°,结合![]() 是
是![]() 的平分线,得∠BAD=∠ABD,即可判断②;过点D作DH⊥AB,由
的平分线,得∠BAD=∠ABD,即可判断②;过点D作DH⊥AB,由![]() ,得:
,得:![]() ,结合CD=HD,即可判断③;根据垂直平分线性质定理的逆定理,即可判断④.
,结合CD=HD,即可判断③;根据垂直平分线性质定理的逆定理,即可判断④.
连接PM,PN,
在APN和APM中,
∵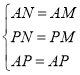 ,
,
∴APNAPM(SSS),
∴∠PAN=∠PAM,
∴![]() 是
是![]() 的平分线,
的平分线,
故①正确;
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴∠BAC=60°,
∵![]() 是
是![]() 的平分线,
的平分线,
∴∠BAD=30°,
∴∠BAD=∠ABD,
∴![]() ,
,
故②正确;
过点D作DH⊥AB,
∵![]() 是
是![]() 的平分线,
的平分线,![]() ,
,
∴CD=HD,
∵∠C=∠BHD=90°
∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
故③正确;
∵AD/span>和BD不一定相等,
∴点![]() 不一定在
不一定在![]() 的垂直平分线上,
的垂直平分线上,
故④错误,
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点,∠F=90°,∠E=30°.
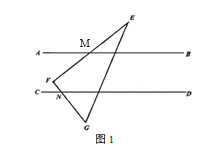
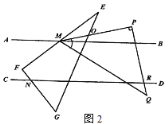
(1)求证:∠EMB+∠DNG=90°
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF的顶点A与D重合,已知∠B=90°,∠BAC=30°,BC=6,∠FDE=90°,DF=DE=4.
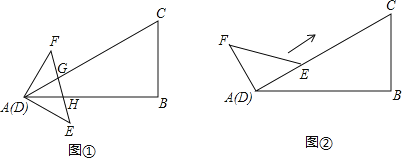
(1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH.设![]() ,在射线DF上取一点P,记:
,在射线DF上取一点P,记: ![]() ,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
(2)在(1)的条件下,求当x为何值时PC//AB;
(3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动![]() 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每天超出计划的量数 |
|
|
|
|
|
|
|
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则二次函数
,则二次函数![]() 的图象与坐标轴的公共点的个数是2或3.
的图象与坐标轴的公共点的个数是2或3.
其中正确的是![]()
A. 只有![]() B. 只有
B. 只有![]() C. 只有
C. 只有![]() D. 只有
D. 只有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
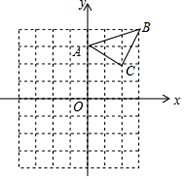
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
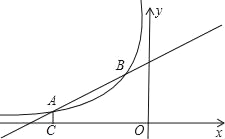
【题目】如图,已知点A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.
(1)求一次函数和反比例函数的解析式;
(2)若P是直线AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com