
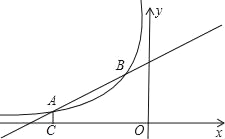
【题目】如图,已知点A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.
(1)求一次函数和反比例函数的解析式;
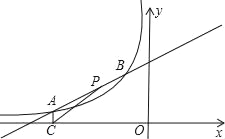
(2)若P是直线AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P的坐标.
,求点P的坐标.
【答案】(1)y=﹣![]() ;y=
;y=![]() x+
x+![]() ;(2)点P的坐标为(﹣2,
;(2)点P的坐标为(﹣2, ![]() )或(﹣6,﹣
)或(﹣6,﹣![]() ).
).
【解析】试题分析:(1)把点B的坐标代入y=![]() 即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
(2)设点P的横坐标为xP,根据点A的坐标可得到AC的长,然后根据条件即可求出xP,然后将xP代入一次函数的解析式就可求出点P的坐标.
试题解析:
(1)把B(﹣1,2)代入y=![]() ,
,
得m=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣![]() ;
;
把A(﹣4,a)代入y=﹣![]() ,得a=
,得a=![]() ,
,
把A(﹣4, ![]() ),B(﹣1,2)代入y=kx+b,得
),B(﹣1,2)代入y=kx+b,得
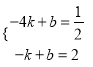 ,
,
解得: 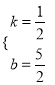 ,
,
∴一次函数解析式为:y=![]() x+
x+![]() ;
;
(2)设点P的横坐标为xP,
∵AC⊥x轴,点A(﹣4, ![]() ),
),
∴AC=![]() .
.
∵△PCA的面积等于![]() ,
,
∴![]() ×
×![]() ×|xP﹣(﹣4)|=
×|xP﹣(﹣4)|=![]() ,
,
解得xP=﹣2或﹣6,
∵P是直线AB上的一点,
∴yP=![]() ×(﹣2)+
×(﹣2)+![]() =
=![]() ,或yP=
,或yP=![]() ×(﹣6)+
×(﹣6)+![]() =﹣
=﹣![]() ,
,
∴点P的坐标为(﹣2, ![]() )或(﹣6,﹣
)或(﹣6,﹣![]() ).
).


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为
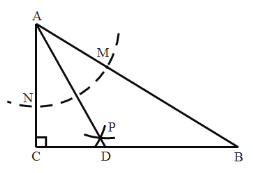
①![]() 是
是![]() 的平分线;
的平分线;
②若![]() ,则
,则![]() ;
;
③![]() ;
;
④点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() 的图象上,点D的坐标为
的图象上,点D的坐标为![]() .将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
.将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种油菜籽在相同条件下的发芽实验结果如表:
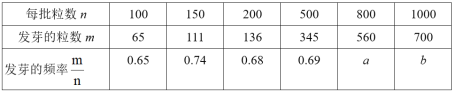
(1)a= ,b= ;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.
(1)若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)超市和姥爷家相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
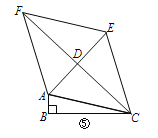
【题目】定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
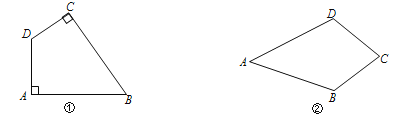
(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);
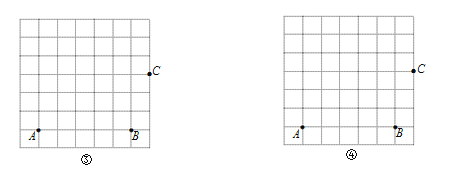
(2)下列说法正确的有 ;(填写所有正确结论的序号)
①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.
①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com