
【题目】某种油菜籽在相同条件下的发芽实验结果如表:
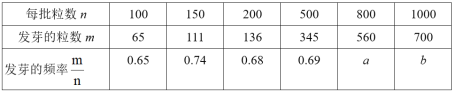
(1)a= ,b= ;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗多少棵?
【答案】(1)0.70,0.70;(2)0.70,理由见解析;(3)6300棵.
【解析】
(1)用发芽的粒数m![]() 每批粒数n即可得到发芽的频率
每批粒数n即可得到发芽的频率![]() ;
;
(2)6批次种子粒数从100粒逐渐增加到1000粒时,种子发芽的频率趋近于![]() ,所以估计当n很大时,频率将接近
,所以估计当n很大时,频率将接近![]() ,由此即可得出答案;
,由此即可得出答案;
(3)首先计算发芽的种子数,然后乘以![]() 即可得.
即可得.
(1)![]() ,
,![]()
故答案为:![]() ,
,![]() ;
;
(2)这种油菜籽发芽的概率估计值是![]()
理由:由表可知,这6批次种子粒数从100粒逐渐增加到1000粒时,种子发芽的频率趋近于![]() ,则种子发芽的频率为
,则种子发芽的频率为![]()
由频率估计概率可得:这种油菜籽发芽的概率估计值是![]() ;
;
(3)这种油菜籽发芽的种子数为![]() (粒)
(粒)
则![]() (棵)
(棵)
答:在相同条件下用10000粒该种油菜籽可得到油菜秧苗6300棵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每天超出计划的量数 |
|
|
|
|
|
|
|
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
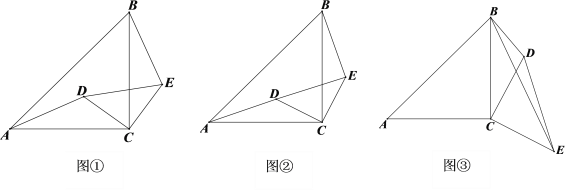
【题目】如图①已知△ACB和△DCE为等腰直角三角形,按如图的位置摆放,直角顶点
C重合.
(1)求证:AD=BE;
(2)将△DCE绕点C旋转得到图②,点A、D、E在同一直线上时,若CD=![]() ,BE=3,
,BE=3,
求AB 的长;
(3)将△DCE绕点C顺时针旋转得到图③,若∠CBD=45°,AC=6,BD=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中![]() 如图
如图![]() ,已知抛物线
,已知抛物线![]() ,经过点
,经过点![]() 、
、![]() .
.

![]() 求此抛物线顶点C的坐标;
求此抛物线顶点C的坐标;
![]() 联结AC交y轴于点D,联结BD、BC,过点C作
联结AC交y轴于点D,联结BD、BC,过点C作![]() ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
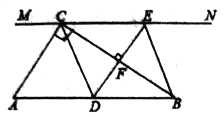
【题目】如图:在Rt△ABC中,∠ACB=90°,过点C的直线MN//AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE.
(1)求点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A= 时,四边形BECD是正方形.说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
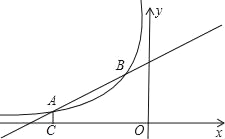
【题目】如图,已知点A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.
(1)求一次函数和反比例函数的解析式;
(2)若P是直线AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道|a|的几何意义是在数轴上数a对应的点与原点的距离,即|a|=|a﹣0|,也就是说,|a|表示在数轴上数a与数0对应点之间的距离.这个结论可以推广为:|a﹣b|表示在数轴上数a与b对应点之间的距离.
例1 已知|a|=2,求a的值.
解:在数轴上与原点距离为2的点的对应数为﹣2和2,即a的值为2和﹣2.
例2 已知|a﹣1|=2,求a的值.
解:在数轴上与1的距离为2点的对应数为3和﹣1,即a的值为3和﹣1.
仿照阅读材料的解法,解决下列问题:
(1)已知|a|=![]() ,求a的值;
,求a的值;
(2)已知|a+2|=4,求a的值;
(3)若数轴上表示a的点在﹣4与2之间,则|a+4|+|a﹣2|的值为 ;
(4)当a满足 时,则|a+4|+|a﹣2|的值最小,最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为32个单位长度,点A在原点的左边,距离原点5个单位长度,点B在原点的右边。
(1)点A所对应的数是___,点B对应的数是___;
(2)若已知在数轴上的点E从点A出发向左运动,速度为每秒2个单位长度,同时点F从点B出发向左运动,速度为每秒4个单位长度,在点C处点F追上了点E,求点C对应的数。
(3)若已知在数轴上的点M从点A出发向右运动,速度为每秒2个单位长度,同时点N从点B出发向右运动,速度为每秒4个单位长度,设线段NO的中点为P(O原点),在运动过程中线段POAM的值是否变化?若不变,求其值;若变化,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
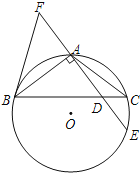
【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.若AF=3,tan∠ABD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com