
����Ŀ����֪�����ϵĵ�A�͵�B֮��ľ���Ϊ32����λ���ȣ���A��ԭ�����ߣ�����ԭ��5����λ���ȣ���B��ԭ����ұߡ�
(1)��A����Ӧ������___����B��Ӧ������___��
(2)����֪�������ϵĵ�E�ӵ�A���������˶����ٶ�Ϊÿ��2����λ���ȣ�ͬʱ��F�ӵ�B���������˶����ٶ�Ϊÿ��4����λ���ȣ��ڵ�C����F���˵�E�����C��Ӧ������
(3)����֪�������ϵĵ�M�ӵ�A���������˶�,�ٶ�Ϊÿ��2����λ����,ͬʱ��N�ӵ�B���������˶�,�ٶ�Ϊÿ��4����λ����,���߶�NO���е�ΪP(Oԭ��)�����˶��������߶�POAM��ֵ�Ƿ�仯?�����䣬����ֵ�����仯����˵�����ɡ�
���𰸡���1��A������Ӧ������5��B��Ӧ������27����2��37����3��![]()
��������
��1�����������ҳ�A��B���Ӧ�������ɣ�
��2���辭��x��F�ϵ�E�����������г����̣�������̵Ľ�õ�x��ֵ������ȷ����C���Ӧ������
��3�����˶�ʱ����t�룬���������г�����t�ķ��̣�������̵Ľ⼴�ɵõ������
(1)��������ã�A������Ӧ������5��B��Ӧ������27��
(2)�辭��x��F�ϵ�E��
��������ã�2x+32=4x��
��ã�x=16��
���C��Ӧ����Ϊ52��16=37��
(3)���˶�ʱ����t��,��AM=2t,PO=![]() ON=
ON=![]() ��
��
��POAMΪ��ֵ,��ֵΪ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����������ʽ��2��![]() ��2��
��2��![]() +1��5��
+1��5��![]() ��5��
��5��![]() +1��������������
+1��������������
���dz�ʹ��ʽa��b��ab+1������һ����������a��b��Ϊ�����������ԡ�����Ϊ��a��b��
��1��ͨ�������ж����ԡ���2��1������4��![]() ���Dz��ǡ������������ԡ���
���Dz��ǡ������������ԡ���
��2������6��a���ǡ������������ԡ�����a��ֵ��
��3������m��n���ǡ������������ԡ�����n����m���� ���������������ԡ�����ǡ����ǡ�������˵�����ɣ�
��4������m��n��������������������������n��1����ֱ���ú�n�Ĵ���ʽ��ʾm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ͳ�������ͬ�����µķ�ѿʵ���������
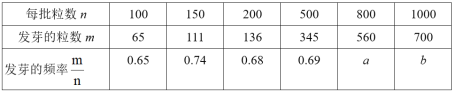
��1��a�� ��b�� ��
��2�������Ͳ��ѷ�ѿ�ĸ��ʹ���ֵ�Ƕ��٣����Ҫ˵�����ɣ�
��3����������Ͳ��ѷ�ѿ��ij�����Ϊ90%��������ͬ��������10000�������Ͳ��ѿɵõ��Ͳ�������ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ��Խ���ֱ�ǵ��ı��ν��������Ρ����������ڱߣ����ظ�����ȵ��ı��ν��������Ρ�����ͼ�٣����ı���ABCD�У�����A����C��90�������ı���ABCD�ǡ����Ρ�����ͼ�ڣ����ı���ABCD�У���AB��AD��BC��DC�����ı���ABCD�ǡ����Ρ���
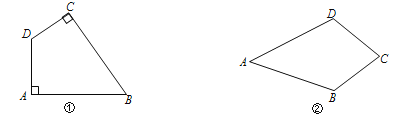
��1����ͼ���ڱ߳�Ϊ1�������������У�A��B��C�ڸ�㣨С�����εĶ��㣩�ϣ���ֱ���ͼ�ۡ�ͼ���л��������Ρ�ABCD�͡����Ρ�ABCD������Ҫ��D��D���ڸ���ϣ���
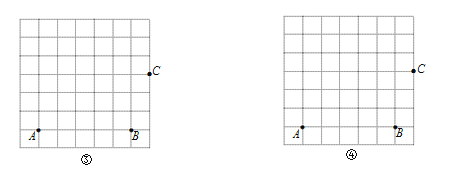
��2������˵����ȷ���� ������д������ȷ���۵���ţ�
��һ��Ա�ƽ�еġ����Ρ��Ǿ��Σ���һ��Ա���ȵġ����Ρ��Ǿ��Σ�
��һ��Ա���ȵġ����Ρ������Σ���һ��Ա�ƽ�еġ����Ρ������Σ�
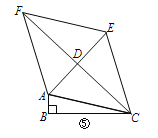
��3����ͼ�����ڡ�ABC�У���ABC��90������ACΪһ�������������Ρ�ACEF����AC��EC��AF��EF��AE��CF���ڵ�D��
������ACE����AFE����֤�������Ρ�ACEF�����Σ�
�������������£�����BD����BD��![]() ����ACB��15������ACD��30������ֱ��д���ı���ACEF�������
����ACB��15������ACD��30������ֱ��д���ı���ACEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ֽƬABCD�У�AB=6��BC=8��
��1��������ֽƬ��BD�۵�����A���ڵ�E������ͼ�٣�����DE��BC�ཻ�ڵ�F����BF�ij���
��2��������ֽƬ�۵���ʹ��B���D�غϣ���ͼ�ڣ������ۺ�GH�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijĦ�г������ܼƻ�ÿ������450��Ħ�г������ڹ���ʵ�����ݣ� ÿ���ϰ�������һ����ȣ�ʵ��ÿ����������ƻ������������±��� [���ӵ�����Ϊ���������ٵ�����Ϊ����]
���� | һ | �� | �� | �� | �� | �� | �� |
���� | ��5 | +7 | ��3 | +4 | +10 | ��9 | ��25 |
��1����������������������Ħ�г���
��2�������ܲ�����ƻ�������ȣ��������˻��Ǽ����ˣ�Ϊʲô?
��3��������������Ȳ������ٵ������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��A��B���㣨��A�ڵ�B����ࣩ����
�ύ��A��B���㣨��A�ڵ�B����ࣩ����![]() �ύ�ڵ�C������ΪD���Գ�����
�ύ�ڵ�C������ΪD���Գ�����![]() �ύ�ڵ�E��ֱ��CE���������ڵ�F�����ڵ�C����ֱ��CD��
�ύ�ڵ�E��ֱ��CE���������ڵ�F�����ڵ�C����ֱ��CD��![]() �ύ�ڵ�G��
�ύ�ڵ�G��
��1����ͼ�٣���ֱ��CE�Ľ���ʽ�Ͷ���D�����ꣻ
��2����ͼ�٣���PΪֱ��CF�Ϸ���������һ�㣬����PC��PF������PCF��������ʱ����M�ǹ�P��ֱ��![]() ���ֱ��l��һ�㣬��N�������߶Գ�����һ�㣬��
���ֱ��l��һ�㣬��N�������߶Գ�����һ�㣬��![]() ����Сֵ��
����Сֵ��
��3����ͼ�ڣ�����D��![]() ��
��![]() ���ڵ�I������GDI������GB����ƽ����
���ڵ�I������GDI������GB����ƽ����![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ������ת��һ������ʱ����
������ת��һ������ʱ����![]() �����I�غϣ�����ת�����е�
�����I�غϣ�����ת�����е�![]() Ϊ
Ϊ![]() ������������ת�����У�ֱ��G����I�����ֱ�x���ֱ��GD���ڵ�K��L���㣬�Ƿ����������K��L��ʹ��GKLΪ�ԡ�LGKΪ�ǵĵ��������Σ������ڣ����ʱGL�ij���
������������ת�����У�ֱ��G����I�����ֱ�x���ֱ��GD���ڵ�K��L���㣬�Ƿ����������K��L��ʹ��GKLΪ�ԡ�LGKΪ�ǵĵ��������Σ������ڣ����ʱGL�ij���



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����ֻװ��2����ɫΧ���Ӻ�1����ɫΧ���ӣ�Χ���ӳ���ɫ���������ͬ����������������������1��Χ���ӣ�������ɫ��Żأ����Ⱥ������������1��Χ���Ӽ�����ɫ�����û���״ͼ�����б����ķ�����������������Χ������ɫ���ǰ�ɫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC��AB=BC����ABΪֱ����Բ��AC�ڵ�D������D�ġ�O�����߽�BC�ڵ�E����CD=5��CE=4�����O�İ뾶��________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com